5a^4 x 3a^2 ÷ 6a^-3
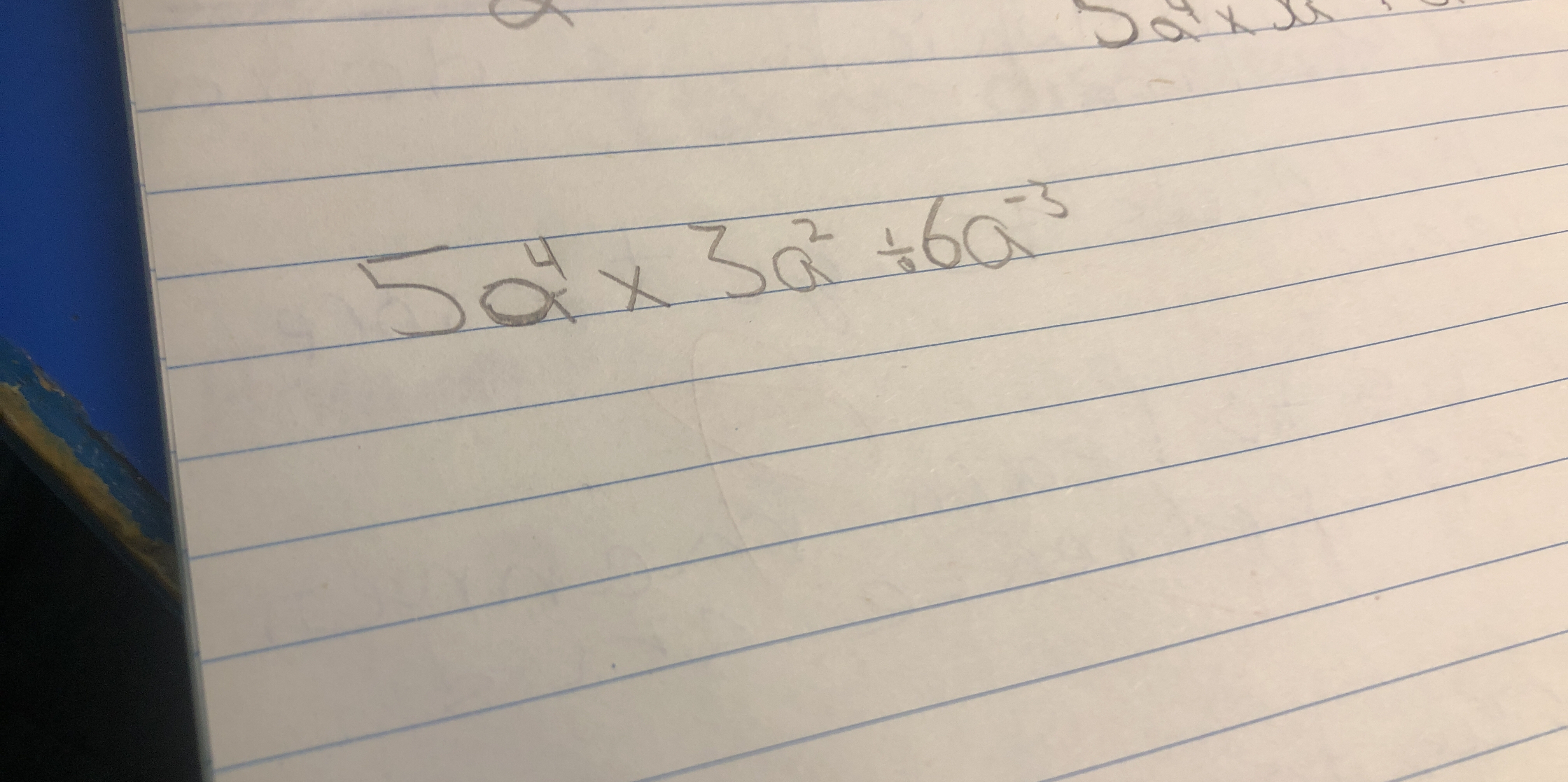
Understand the Problem
The question seems to be asking how to simplify or solve the expression involving exponents and multiplication of variables, specifically 5a^4 x 3a^2 ÷ 6a^-3.
Answer
The simplified result is $$ \frac{5}{2}a^9 $$.
Answer for screen readers
The final answer is $$ \frac{5}{2}a^9 $$.
Steps to Solve
-
Multiply the coefficients and add the exponents
Start with multiplying the coefficients (5 and 3) and then apply the exponent rule, which states that when multiplying like bases, you add the exponents.
$$ 5a^4 \times 3a^2 = (5 \times 3)(a^{4+2}) = 15a^6 $$ -
Set up the division with the new expression
Now replace the original expression with the result of the multiplication. You will also divide it by $6a^{-3}$:
$$ \frac{15a^6}{6a^{-3}} $$ -
Divide the coefficients and subtract the exponents
Divide the coefficients (15 and 6) and apply the exponent rule by subtracting the exponents for like bases.
$$ \frac{15}{6} \times a^{6 - (-3)} = \frac{15}{6} \times a^{6 + 3} = \frac{15}{6} \times a^{9} $$ -
Simplify the fraction
The fraction $\frac{15}{6}$ can be simplified.
$$ \frac{15}{6} = \frac{5}{2} $$ -
Write the final expression
Combining everything above gives the final answer:
$$ \frac{5}{2}a^9 $$
The final answer is $$ \frac{5}{2}a^9 $$.
More Information
This expression represents the simplified form of the original problem, showing how coefficients and exponents combine through multiplication and division.
Tips
- Confusing the rules for multiplying and dividing exponents.
- Avoid this: Remember that when multiplying like bases, add the exponents; when dividing, subtract the exponents.
- Forgetting to simplify the coefficients after division.
AI-generated content may contain errors. Please verify critical information