5^4 x 3a^2 ÷ a^-3
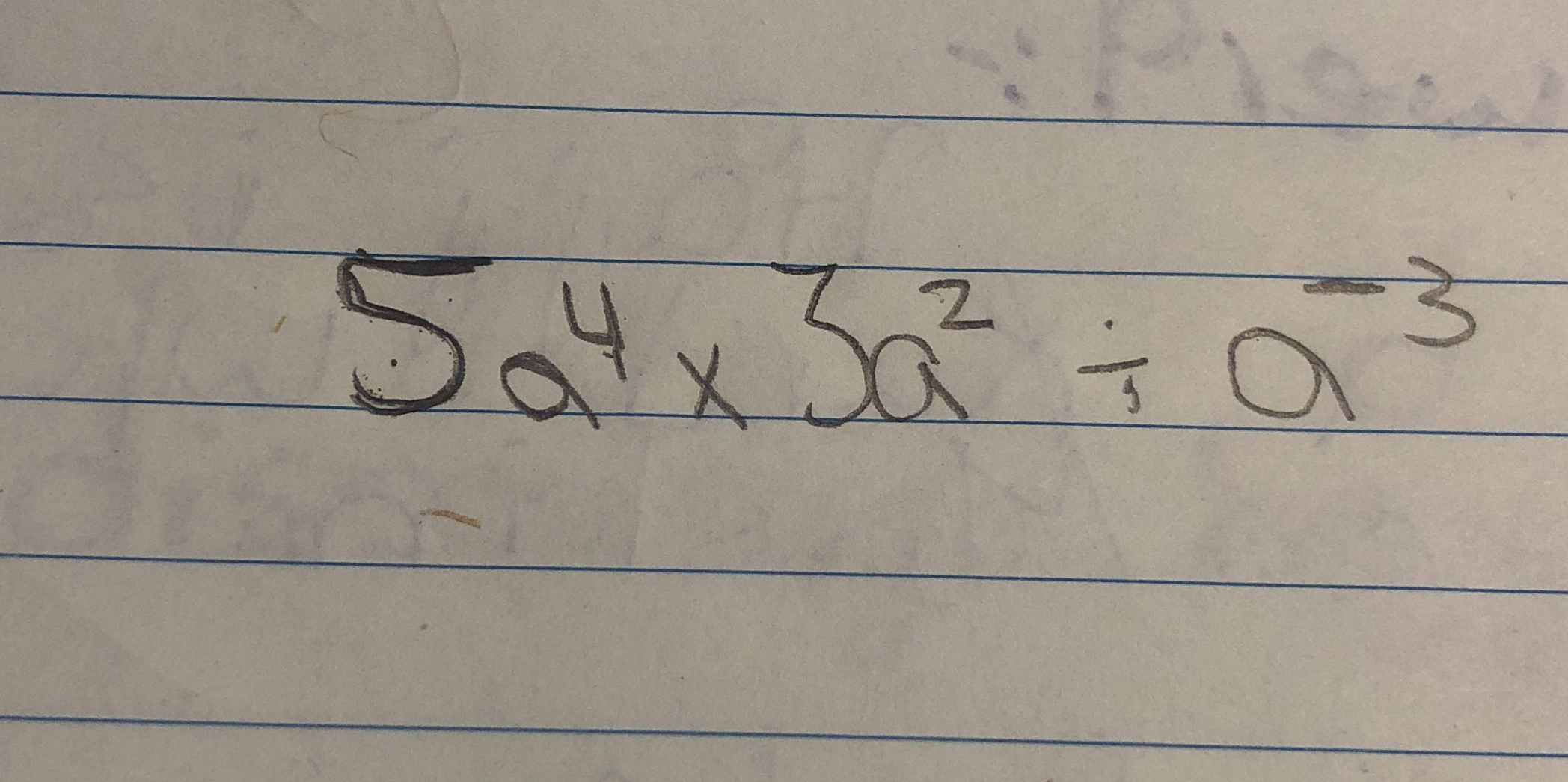
Understand the Problem
The question is asking us to simplify the expression involving variables and exponentiation: 5^4 x 3a^2 ÷ a^-3. We will need to use the laws of exponents to simplify this expression correctly.
Answer
The simplified expression is \(1875a^5\).
Answer for screen readers
The simplified expression is (1875a^5).
Steps to Solve
-
Calculate (5^4) First, we calculate the exponent:
$$ 5^4 = 5 \times 5 \times 5 \times 5 = 625 $$ -
Express the multiplication and division We now rewrite the expression using the value from the first step:
$$ 625 \times 3a^2 \div a^{-3} $$ -
Combine (a^2) and (a^{-3}) using the laws of exponents Using the rule that $a^m \div a^n = a^{m-n}$, we combine the terms: $$ a^2 \div a^{-3} = a^{2 - (-3)} = a^{2 + 3} = a^5 $$
-
Combine (625) and (3) Now, we multiply the coefficients 625 and 3:
$$ 625 \times 3 = 1875 $$ -
Final expression Putting all the calculations together, we have:
$$ 1875a^5 $$
The simplified expression is (1875a^5).
More Information
This expression combines constants and variables using the laws of exponents. Remember that when you divide two expressions with the same base, you subtract the exponents.
Tips
- Confusing negative exponents: Remember that $a^{-n} = \frac{1}{a^n}$.
- Forgetting to combine like terms: Always pay attention to combining constant coefficients and variables correctly.
AI-generated content may contain errors. Please verify critical information