5(3 - 2i)² · (i / (i - 2)) = ?
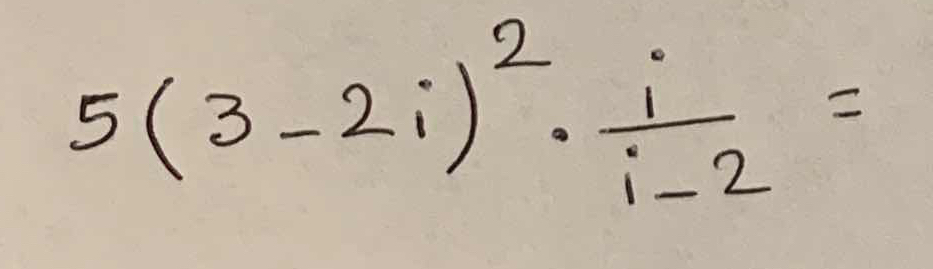
Understand the Problem
The question is asking to simplify the expression involving complex numbers and division. We will square the term (3 - 2i), multiply it by 5, and then multiply by the result of the division involving 'i' and (i - 2).
Answer
The result is $$ \frac{101 - 242i}{4} $$
Answer for screen readers
The final answer is
$$ \frac{101 - 242i}{4} $$
Steps to Solve
- Square the complex number (3 - 2i)
To find ((3 - 2i)^2), use the formula ((a - b)^2 = a^2 - 2ab + b^2). Here, (a = 3) and (b = 2i).
Calculating:
$$ (3 - 2i)^2 = 3^2 - 2(3)(2i) + (2i)^2 $$
This simplifies to:
$$ = 9 - 12i - 4 = 5 - 12i $$
- Multiply the squared result by 5
Next, we multiply the result we got from the previous step by 5:
$$ 5(5 - 12i) = 25 - 60i $$
- Calculate ( \frac{i}{i - 2} )
To simplify ( \frac{i}{i - 2} ), multiply the numerator and the denominator by the conjugate of the denominator, (i + 2):
$$ \frac{i(i + 2)}{(i - 2)(i + 2)} = \frac{i^2 + 2i}{i^2 - 4} $$
Since (i^2 = -1):
$$ = \frac{-1 + 2i}{-4} = \frac{1 - 2i}{4} $$
- Combine both parts together
Now we combine (25 - 60i) and (\frac{1 - 2i}{4}):
First, rewrite (25 - 60i) as a fraction with a denominator of 4:
$$ = \frac{(25 - 60i) \cdot 4}{4} = \frac{100 - 240i}{4} $$
Now, sum the two fractions:
$$ \frac{100 - 240i + 1 - 2i}{4} = \frac{101 - 242i}{4} $$
Thus, the final answer is:
$$ \frac{101 - 242i}{4} $$
The final answer is
$$ \frac{101 - 242i}{4} $$
More Information
This result combines the complex numbers and follows the rules for multiplying and simplifying expressions with imaginary units.
Tips
- Forgetting to use the conjugate of the denominator when simplifying complex fractions.
- Miscalculating powers of complex numbers; careful with signs when using (i^2).
- Not simplifying the final expression properly.
AI-generated content may contain errors. Please verify critical information