4n^2 + 3n - 27 / 8n^2 - 24n + 108

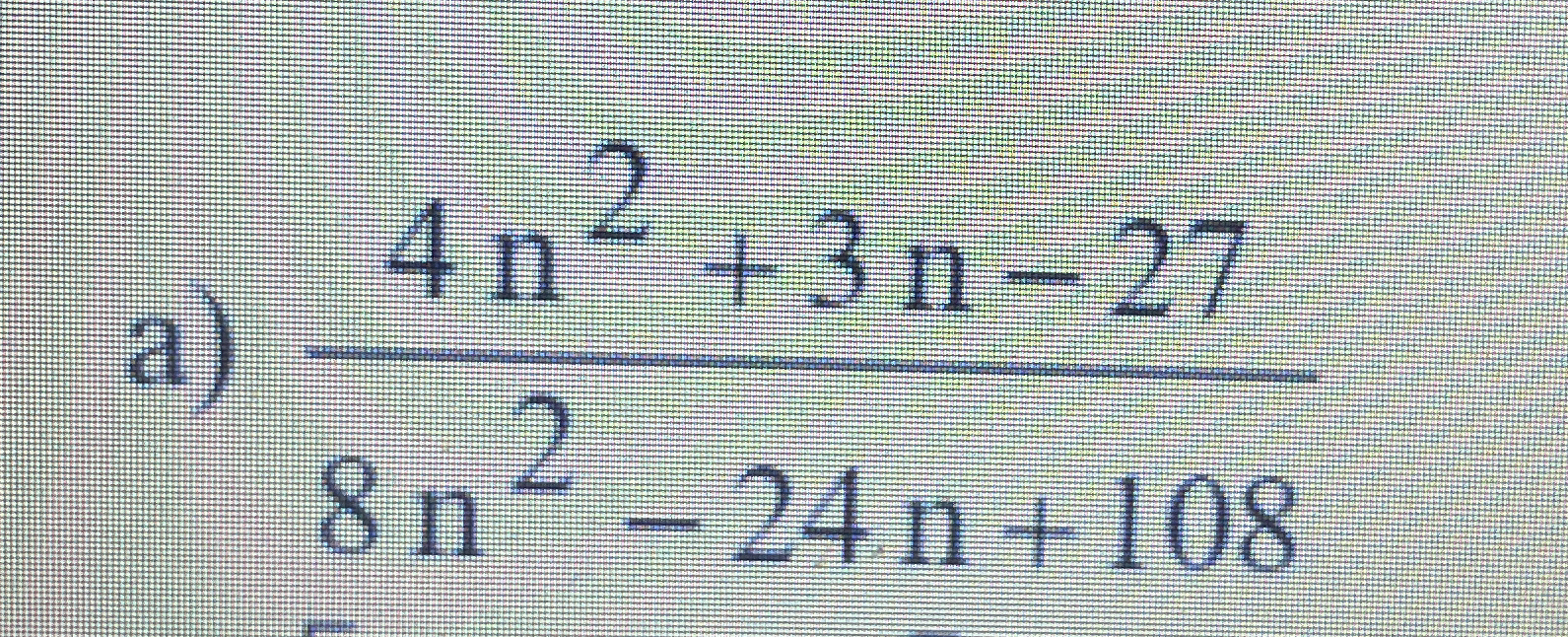
Understand the Problem

The question presents a mathematical expression involving a fraction with polynomials in the numerator and denominator. It is asking for a solution or simplification of this expression.

Answer

$$ \frac{(4n - 9)(n + 3)}{(n - 9)(2n - 3)} $$

Steps to Solve

Factor the Numerator To factor the numerator (4n^2 + 3n - 27), we look for two numbers that multiply to (4 \times (-27) = -108) and add to (3). The numbers (12) and (-9) work. Therefore, we rewrite it as: $$ 4n^2 + 12n - 9n - 27 = 4n(n + 3) - 9(n + 3) $$ This can be factored as: $$ (4n - 9)(n + 3) $$
Factor the Denominator Next, we factor the denominator (8n^2 - 24n + 108). We find two numbers that multiply to (8 \times 108 = 864) and add to (-24). The numbers are (-12) and (-12), so we rewrite as: $$ 8n^2 - 12n - 12n + 108 = 4n(2n - 3) - 36(2n - 3) $$ This can be factored as: $$ (4n - 36)(2n - 3) $$
Simplify the Expression The fraction can now be written as: $$ \frac{(4n - 9)(n + 3)}{(4n - 36)(2n - 3)} $$ Notice that (4n - 36) can be factored as (4(n - 9)), making the expression: $$ \frac{(4n - 9)(n + 3)}{4(n - 9)(2n - 3)} $$
Cancel Common Factors We simplify the fraction by canceling the common factor (4) from numerator and denominator. Resulting in: $$ \frac{(4n - 9)(n + 3)}{(n - 9)(2n - 3)} $$

The simplified form of the expression is: $$ \frac{(4n - 9)(n + 3)}{(n - 9)(2n - 3)} $$

More Information

This fraction represents a rational expression that simplifies the original polynomial expression. Simplifying rational expressions is crucial in algebra, as it allows for easier manipulation and solving of equations.

Tips

Ignoring Negative Signs: Always check for correct signs when factoring.
Failing to Look for Common Factors: Make sure to check for and simplify any common factors in the numerator and denominator.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!