-4/3 ÷ (-2/5)
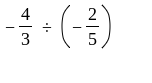
Understand the Problem
The question presents a mathematical expression involving fractions, division, and parentheses. We need to solve the expression step by step.
Answer
The answer is $\frac{10}{3}$.
Answer for screen readers
The final answer is $\frac{10}{3}$.
Steps to Solve
- Identify the operation
We need to perform division with two fractions: $$ -\frac{4}{3} \div -\frac{2}{5} $$
- Convert division to multiplication
To divide by a fraction, we multiply by its reciprocal: $$ -\frac{4}{3} \times -\frac{5}{2} $$
- Multiply the fractions
Now we multiply the numerators and the denominators: $$ \text{Numerator: } -4 \times -5 = 20 $$ $$ \text{Denominator: } 3 \times 2 = 6 $$
So, we get: $$ \frac{20}{6} $$
- Simplify the fraction
Now we simplify $$ \frac{20}{6} $$ by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 2: $$ \frac{20 \div 2}{6 \div 2} = \frac{10}{3} $$
- Final Result
The final simplified answer is: $$ \frac{10}{3} $$
The final answer is $\frac{10}{3}$.
More Information
The result $\frac{10}{3}$ represents a fraction that cannot be further simplified, and it can also be expressed as a mixed number: $3 \frac{1}{3}$. This operation illustrates how division of fractions works by converting division to multiplication with the reciprocal.
Tips
- Mistaking Division Signs: Peple often forget that dividing by a negative leads to a positive when both terms are negative.
- Not Simplifying: Sometimes, students skip the simplification step, leaving their answer in an unformatted state.
