4√3 + 2√12
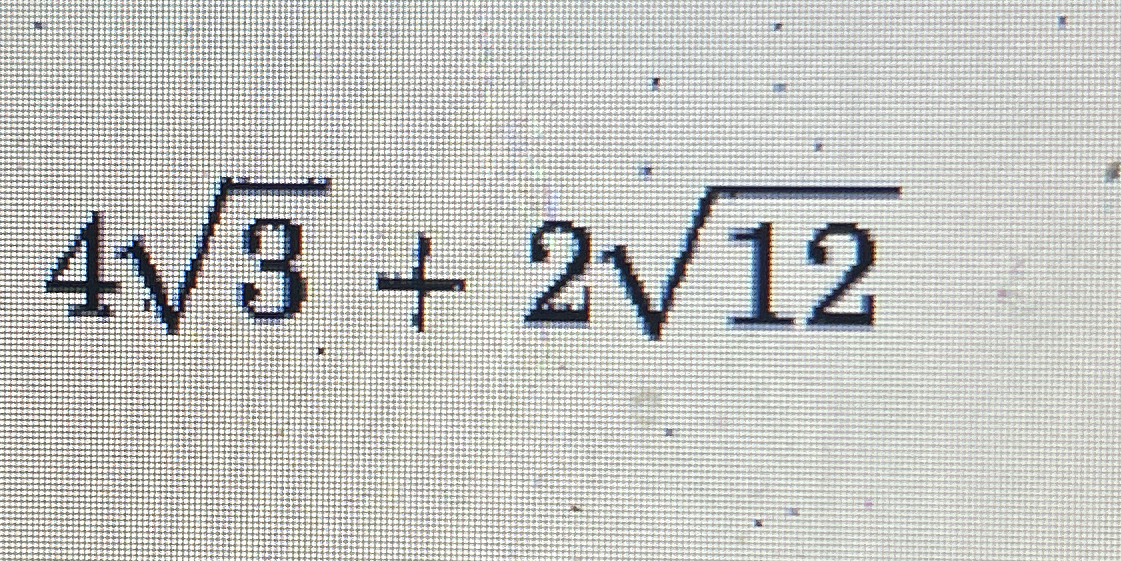
Understand the Problem
The question involves the expression 4√3 + 2√12, requiring simplification of the square roots and combining like terms.
Answer
The final answer is \( 8\sqrt{3} \).
Answer for screen readers
The simplified expression is ( 8\sqrt{3} ).
Steps to Solve
- Simplify the square root of 12
The square root of 12 can be simplified as follows:
$$ \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} $$
Thus,
$$ 2\sqrt{12} = 2 \times 2\sqrt{3} = 4\sqrt{3} $$
- Combine like terms
Now, substitute $2\sqrt{12}$ back into the original expression:
$$ 4\sqrt{3} + 2\sqrt{12} = 4\sqrt{3} + 4\sqrt{3} $$
Combine the like terms:
$$ 4\sqrt{3} + 4\sqrt{3} = 8\sqrt{3} $$
- Final expression
The final expression is:
$$ 8\sqrt{3} $$
The simplified expression is ( 8\sqrt{3} ).
More Information
In this problem, we simplified square roots and combined like terms. Simplifying square roots is a fundamental algebraic skill that can be useful in various mathematical contexts.
Tips
A common mistake is failing to simplify the square root correctly. It's important to break down the number under the square root into its prime factors to simplify it accurately.
AI-generated content may contain errors. Please verify critical information