∫ (3x² + 4x + 1) / (3x³ + 6x² + 3x + 5) dx = ?
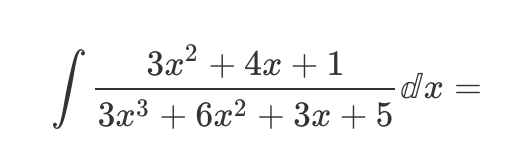
Understand the Problem
The question is asking for the integral of a rational function involving polynomials. Specifically, we need to find the indefinite integral of the given expression with respect to x.
Answer
$$ \int \frac{3x^2 + 4x + 1}{3x^3 + 6x^2 + 3x + 5} \, dx = \frac{1}{3} \ln |3x^3 + 6x^2 + 3x + 5| + C $$
Answer for screen readers
$$ \int \frac{3x^2 + 4x + 1}{3x^3 + 6x^2 + 3x + 5} , dx = \frac{1}{3} \ln |3x^3 + 6x^2 + 3x + 5| + C $$
Steps to Solve
- Identify the Integral We need to evaluate the integral
$$ \int \frac{3x^2 + 4x + 1}{3x^3 + 6x^2 + 3x + 5} , dx $$
-
Check Polynomial Degrees The degree of the numerator (2) is less than the degree of the denominator (3). Since the degree of the numerator is less than the degree of the denominator, we can proceed with direct integration.
-
Perform Polynomial Long Division (if necessary) In this case, the degree of the numerator is less than the denominator, so we don't need to perform polynomial long division.
-
Substitution for Integration We can use the substitution method by letting
$$ u = 3x^3 + 6x^2 + 3x + 5 $$
Next, differentiate $u$ with respect to $x$:
$$ \frac{du}{dx} = 9x^2 + 12x + 3 $$
This means:
$$ du = (9x^2 + 12x + 3) , dx $$
- Express the Integral in terms of $u$ Now, express the integral in terms of $u$. The numerator can be adjusted:
$$ 3x^2 + 4x + 1 = \frac{1}{3}(9x^2 + 12x + 3) - \frac{1}{3} $$
So, the integral becomes:
$$ \int \frac{1}{3} \left( \frac{(9x^2 + 12x + 3) - 1}{u} \right) du $$
- Separate the Integral This can be separated into two integrals:
$$ \frac{1}{3} \int \frac{9x^2 + 12x + 3}{u} , du - \frac{1}{3} \int \frac{1}{u} , du $$
- Integrate Each Part Now, integrate:
- The first part becomes:
$$ \frac{1}{3} \ln |u| $$
- And the second part becomes:
$$ \frac{1}{3} \ln |u| $$
Thus, we have:
$$ \int \frac{3x^2 + 4x + 1}{3x^3 + 6x^2 + 3x + 5} , dx = \frac{1}{3} \ln |u| + C $$
- Back Substitution Replace $u$ with the original polynomial:
$$ \int \frac{3x^2 + 4x + 1}{3x^3 + 6x^2 + 3x + 5} , dx = \frac{1}{3} \ln |3x^3 + 6x^2 + 3x + 5| + C $$
$$ \int \frac{3x^2 + 4x + 1}{3x^3 + 6x^2 + 3x + 5} , dx = \frac{1}{3} \ln |3x^3 + 6x^2 + 3x + 5| + C $$
More Information
The integral of a rational function, where the degree of the numerator is less than the degree of the denominator, can often be simplified using substitution. In this case, we used a polynomial expression to change the form of the integral, allowing easier integration.
Tips
- Not Checking Degrees: Failing to check the degrees of the polynomials can lead to incorrect methodology; always confirm that the numerator's degree is less than the denominator's degree for direct integration.
- Incorrect Substitution: It's important to differentiate properly when substituting. Ensure that $du$ is correctly derived from your substitution.
AI-generated content may contain errors. Please verify critical information