(-3p^3 + 5p^2 - 2p) + (-p^3 - 8p^2 - 15p) =
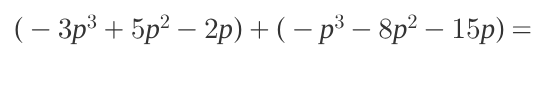
Understand the Problem
The question requires combining like terms from two polynomial expressions. We need to add the coefficients of the terms with the same power of 'p'.
Answer
$-4p^3 - 3p^2 - 17p$
Answer for screen readers
$-4p^3 - 3p^2 - 17p$
Steps to Solve
- Identify like terms
Identify terms with the same power of $p$ in both polynomials. We have $p^3$ terms, $p^2$ terms, and $p$ terms.
- Combine the $p^3$ terms
Add the coefficients of the $p^3$ terms: $$ -3p^3 + (-p^3) = -3p^3 - p^3 = (-3 - 1)p^3 = -4p^3 $$
- Combine the $p^2$ terms
Add the coefficients of the $p^2$ terms: $$ 5p^2 + (-8p^2) = 5p^2 - 8p^2 = (5 - 8)p^2 = -3p^2 $$
- Combine the $p$ terms
Add the coefficients of the $p$ terms: $$ -2p + (-15p) = -2p - 15p = (-2 - 15)p = -17p $$
- Write the simplified polynomial
Combine the results from the previous steps to form the simplified polynomial: $$ -4p^3 - 3p^2 - 17p $$
$-4p^3 - 3p^2 - 17p$
More Information
The problem involves combining like terms in polynomials. Like terms are terms that have the same variable raised to the same power.
Tips
A common mistake is to incorrectly add or subtract the coefficients, especially when dealing with negative numbers. Another mistake is to combine terms with different powers of the variable. For example, adding a $p^3$ term to a $p^2$ term. Make sure to only combine terms that have the exact same variable and exponent.
AI-generated content may contain errors. Please verify critical information