3i^3(i - 2) - 3i =
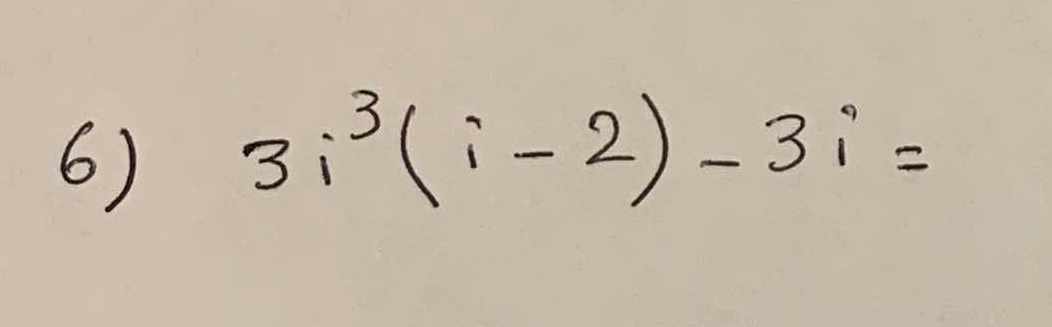
Understand the Problem
The question requires evaluating the expression involving imaginary numbers, specifically simplifying the expression 3i^3(i - 2) - 3i.
Answer
The simplified expression is \( 3 + 3i \).
Answer for screen readers
The simplified expression is ( 3 + 3i ).
Steps to Solve
- Calculate $i^3$
Recall that ( i^2 = -1 ). Therefore, ( i^3 = i^2 \cdot i = -1 \cdot i = -i ).
- Substitute $i^3$ into the expression
Replace ( i^3 ) in the original expression: $$ 3i^3(i - 2) - 3i = 3(-i)(i - 2) - 3i $$
- Distribute $3(-i)$
Now, distribute ( 3(-i) ) into ( (i - 2) ): $$ 3(-i)(i) - 3(-i)(2) - 3i = -3i^2 + 6i - 3i $$
- Simplify $-3i^2$
Since ( i^2 = -1 ): $$ -3i^2 = -3(-1) = 3 $$
- Combine like terms
Add the terms together: $$ 3 + 6i - 3i = 3 + 3i $$
The simplified expression is ( 3 + 3i ).
More Information
The expression ( 3 + 3i ) indicates that there is a real part (3) and an imaginary part (3i). Imaginary numbers are often used in complex number calculations and have applications in engineering and physics.
Tips
- Confusing ( i^3 ) with ( i^2 ): Remember that ( i^3 = -i ), not ( i ).
- Forgetting to distribute properly when multiplying terms.
AI-generated content may contain errors. Please verify critical information