3/5(x - 12) = -4(x + 9) + 1
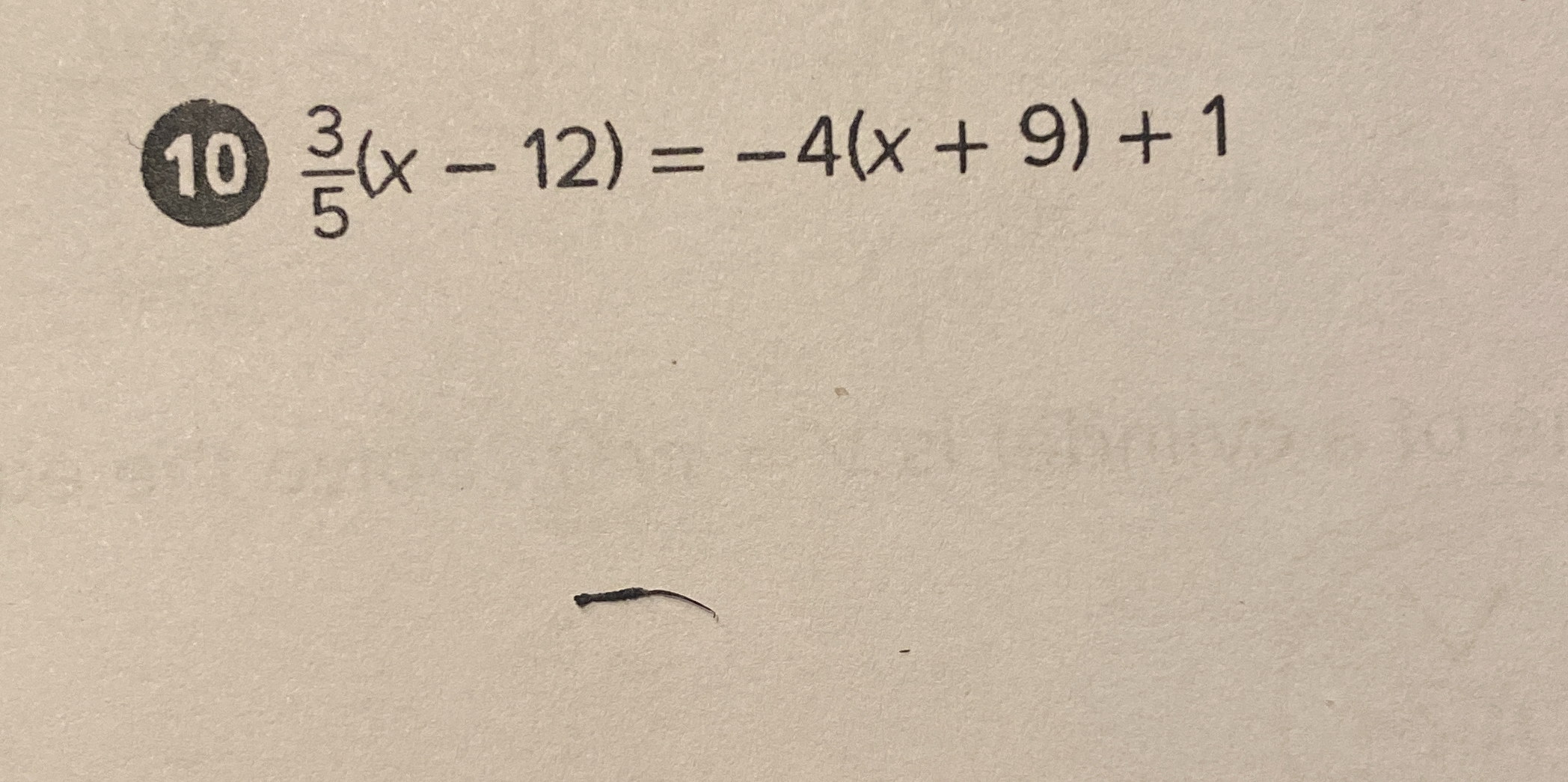
Understand the Problem
The question is asking to solve the equation involving fractions and variables. It requires manipulating both sides of the equation to isolate the variable, which will typically include expanding terms and combining like terms.
Answer
The value of \(x\) is \( x = \frac{-139}{23} \) or approximately \( -6.04 \).
Answer for screen readers
The final answer is ( x = \frac{-139}{23} ) or approximately ( -6.04 ).
Steps to Solve
-
Distribute on both sides Expand both sides of the equation:
The left side: $$ \frac{3}{5}(x - 12) = \frac{3}{5}x - \frac{36}{5} $$
The right side: $$ -4(x + 9) + 1 = -4x - 36 + 1 = -4x - 35 $$
Now the equation becomes: $$ \frac{3}{5}x - \frac{36}{5} = -4x - 35 $$
-
Eliminate fractions Multiply the entire equation by 5 to eliminate the fraction: $$ 5 \left( \frac{3}{5}x - \frac{36}{5} \right) = 5 \left(-4x - 35\right) $$
This simplifies to: $$ 3x - 36 = -20x - 175 $$
-
Rearrange the equation Move all terms involving (x) to one side and constant terms to the other: $$ 3x + 20x = -175 + 36 $$
This simplifies to: $$ 23x = -139 $$
-
Solve for (x) Divide by 23 to isolate (x): $$ x = \frac{-139}{23} $$
-
Simplify the fraction To find the decimal or simplest form: $$ x = -6.04 $$ (approximately)
The final answer is ( x = \frac{-139}{23} ) or approximately ( -6.04 ).
More Information
This equation demonstrates how to manipulate fractions and apply distribution and combination of like terms. Understanding these steps is crucial for solving linear equations.
Tips
- Forgetting to apply distribution correctly when expanding terms.
- Neglecting to combine like terms when rearranging the equation.
- Incorrectly eliminating fractions, such as forgetting to multiply all terms in the equation by the same factor.
AI-generated content may contain errors. Please verify critical information