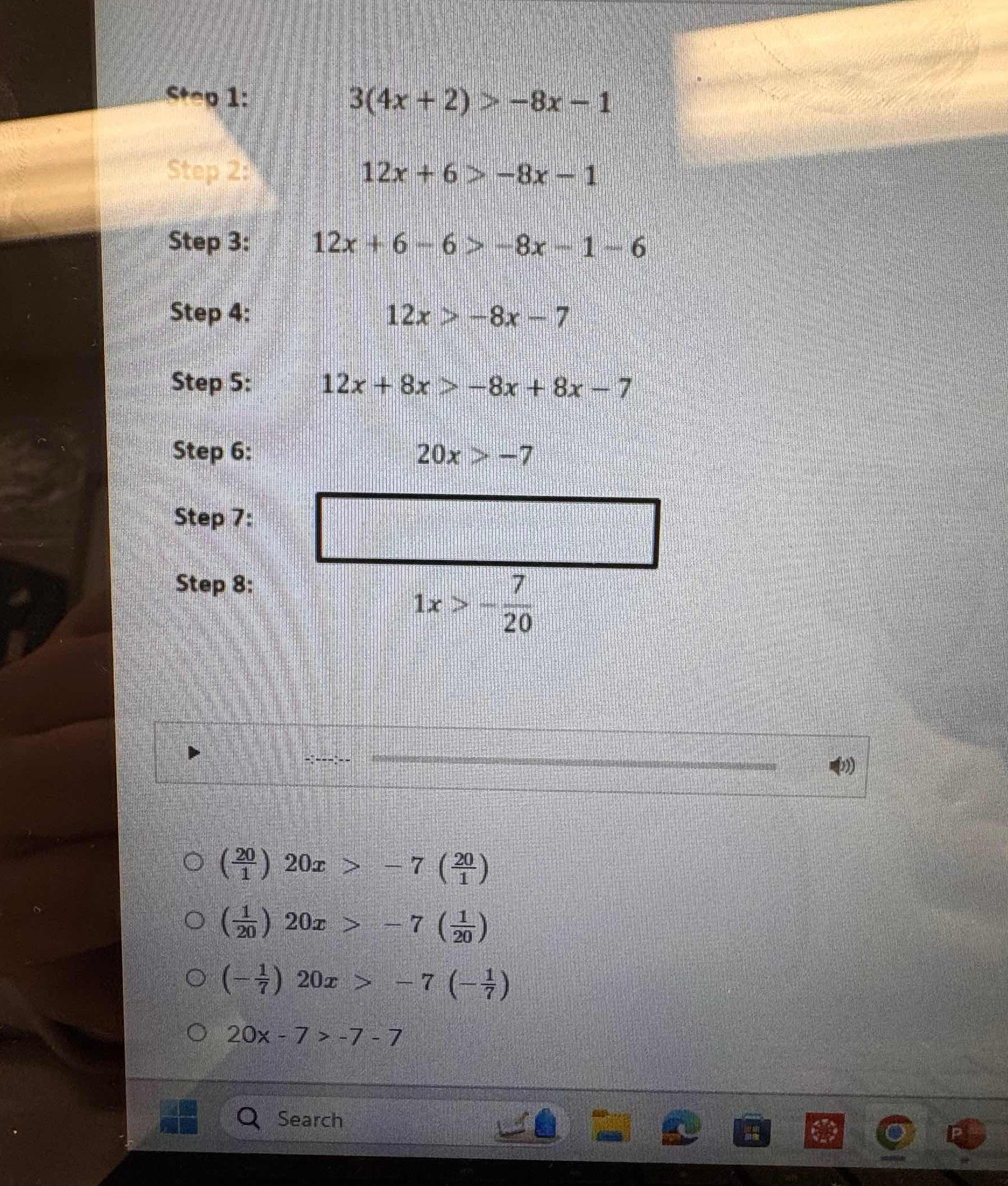
3(4x + 2) > -8x - 1
Understand the Problem
The question involves solving an inequality step by step. It follows an equation involving x and requires us to determine how to further manipulate the equation based on provided steps and options.
Answer
$$ x > -\frac{7}{20} $$
Answer for screen readers
The solution is
$$ x > -\frac{7}{20} $$
Steps to Solve
- Distribute on the left side
Start by distributing the 3 into the parentheses on the left side of the inequality.
$$ 3(4x + 2) > -8x - 1 $$
Becomes:
$$ 12x + 6 > -8x - 1 $$
- Move constants to one side
Next, add 1 to both sides to get all constants on one side:
$$ 12x + 6 + 1 > -8x $$
Which simplifies to:
$$ 12x + 7 > -8x $$
- Combine like terms
Now, add $8x$ to both sides to combine the $x$ terms:
$$ 12x + 8x + 7 > -8x + 8x $$
This simplifies to:
$$ 20x + 7 > 0 $$
- Isolate the variable term
Next, subtract 7 from both sides to isolate the term with $x$:
$$ 20x > -7 $$
- Solve for x
Finally, divide both sides by 20 to solve for $x$:
$$ x > -\frac{7}{20} $$
The solution is
$$ x > -\frac{7}{20} $$
More Information
This inequality indicates that $x$ must be greater than $-\frac{7}{20}$. This means any number greater than $-\frac{7}{20}$ satisfies the condition.
Tips
- Misapplying inequalities: Remember, when multiplying or dividing by a negative number, you must flip the inequality sign. Here, we only divided by a positive number, so the sign stays the same.
- Combining like terms incorrectly: Carefully combine $x$ terms to avoid errors in equations.
AI-generated content may contain errors. Please verify critical information