3√13 + 7√13
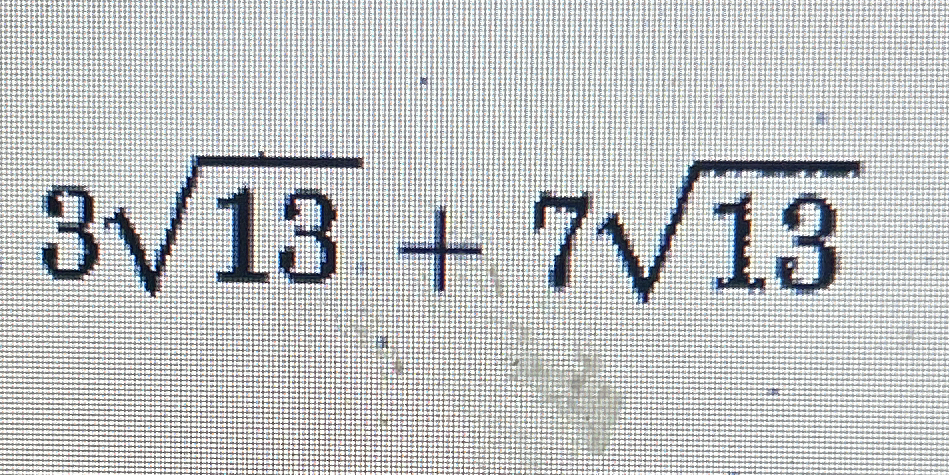
Understand the Problem
The question is asking us to simplify the expression involving the square roots of 13, specifically to combine the terms 3√13 and 7√13.
Answer
The simplified expression is $10\sqrt{13}$.
Answer for screen readers
The simplified expression is $10\sqrt{13}$.
Steps to Solve
-
Identify like terms We can see that both terms involve the square root of 13. We can treat $\sqrt{13}$ as a variable, allowing us to combine the coefficients.
-
Combine the coefficients The terms are $3\sqrt{13}$ and $7\sqrt{13}$. To combine them, we add the coefficients (3 and 7): $$ 3 + 7 = 10 $$
-
Rewrite the expression Now we rewrite the original expression using the combined coefficient: $$ 3\sqrt{13} + 7\sqrt{13} = 10\sqrt{13} $$
The simplified expression is $10\sqrt{13}$.
More Information
Combining like terms is a fundamental skill in algebra, especially when dealing with expressions that contain square roots or variables. In this case, we were able to simplify the expression directly by treating $\sqrt{13}$ as a common factor.
Tips
- Forgetting to combine the coefficients correctly, which can lead to an incorrect final answer. Always double-check your arithmetic when adding or subtracting coefficients.
AI-generated content may contain errors. Please verify critical information