3(1 - (w + 3)) + 4w or -3(3 - 3(w - 5)) + 6w
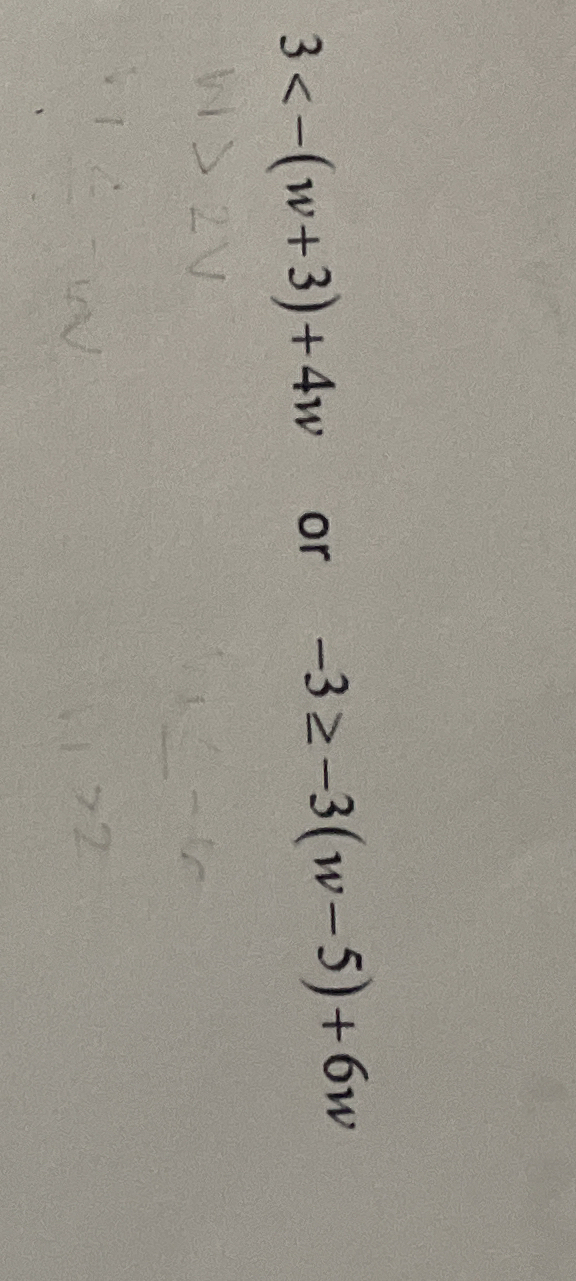
Understand the Problem
The question involves simplifying two algebraic expressions and possibly setting them equal to each other to solve for the variable w. The first expression is 3(1 - (w + 3)) + 4w, and the second expression is -3(3 - 3(w - 5)) + 6w. The goal is to manipulate these expressions according to the rules of algebra.
Answer
The value of \( w \) is \( \frac{24}{7} \).
Answer for screen readers
The value of ( w ) is
$$ w = \frac{24}{7} $$
Steps to Solve
- Simplify the first expression
Start with the first expression:
$$ 3(1 - (w + 3)) + 4w $$
Distribute the $3$:
$$ 3 \cdot 1 - 3 \cdot (w + 3) + 4w = 3 - 3w - 9 + 4w $$
Combine like terms:
$$ 3 - 9 + (-3w + 4w) = -6 + w $$
So the first expression simplifies to:
$$ w - 6 $$
- Simplify the second expression
Now simplify the second expression:
$$ -3(3 - 3(w - 5)) + 6w $$
First, simplify inside the parentheses:
$$ -3(3 - 3w + 15) + 6w = -3(18 - 3w) + 6w $$
Distribute the $-3$:
$$ -54 + 9w + 6w = -54 + 15w $$
So the second expression simplifies to:
$$ 15w - 54 $$
- Set the expressions equal to each other
Now we set the two simplified expressions equal to each other:
$$ w - 6 = 15w - 54 $$
- Solve for ( w )
Rearranging the equation:
$$ -6 + 54 = 15w - w $$
This simplifies to:
$$ 48 = 14w $$
Now, divide both sides by $14$ to solve for $w$:
$$ w = \frac{48}{14} = \frac{24}{7} $$
The value of ( w ) is
$$ w = \frac{24}{7} $$
More Information
The solution shows how algebraic expressions can be simplified and solved step by step. The value ( w = \frac{24}{7} ) can also be converted to a decimal, approximately ( 3.43 ).
Tips
- Distributing incorrectly: Make sure to multiply all terms inside the parentheses with the factor outside correctly.
- Combining like terms incorrectly: Always leave an eye on combining terms with the same variable and constant terms separately.
AI-generated content may contain errors. Please verify critical information