(3) 8/15 [ ] 8/17
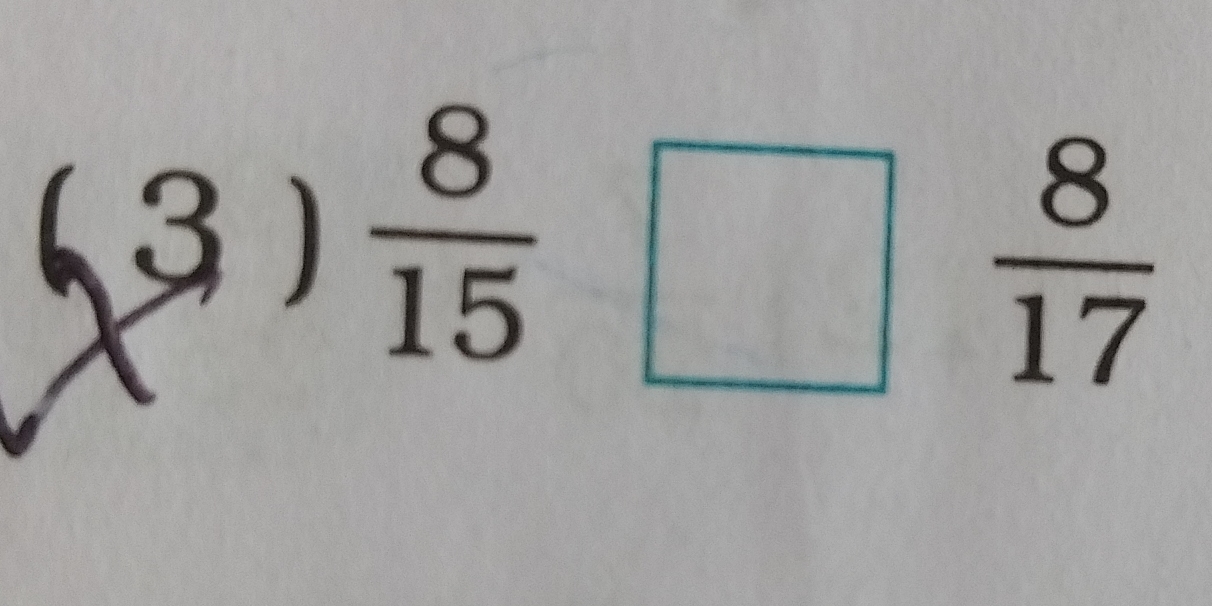
Understand the Problem
The question involves a mathematical operation where we need to find out what operation or value fits in the blank square next to the fractions 8/15 and 8/17, given the context provided by the initial (3).
Answer
The missing value is \( 16 \).
Answer for screen readers
The missing value is ( 16 ).
Steps to Solve
-
Identify the Sequence We need to determine the missing operation or value between the fractions ( \frac{8}{15} ) and ( \frac{8}{17} ).
-
Look for a Pattern Notice that both fractions have the same numerator of 8. The denominators are 15 and 17. There appears to be a simple pattern as these numbers progress.
-
Finding the Relationship Calculate how the denominators relate to each other. If we look at the differences, we see: $$ 17 - 15 = 2 $$
-
Estimate Possible Operations Given the relationship observed, we can hypothesize an operation or value placed in the blank. Since the denominators are increasing, we might be looking at the average or some operation that involves finding a value between the two fractions.
-
Calculate the Average Denominator To find an average value, we could average the two denominators: $$ \text{Average} = \frac{15 + 17}{2} = \frac{32}{2} = 16 $$
-
Conclude the Value The value that fits in the blank can logically be 16 as it lies between the two denominators.
The missing value is ( 16 ).
More Information
The fractions ( \frac{8}{15} ) and ( \frac{8}{17} ) suggest a simple pattern of increasing denominators. The average of 15 and 17 gives us a rational number that fits neatly in the series, adding a layer of understanding to the operations.
Tips
- Confusing the average with other operations like multiplication or addition of the denominators directly.
- Not recognizing that the missing value corresponds logically to the mathematical relationship between the fractions.
AI-generated content may contain errors. Please verify critical information