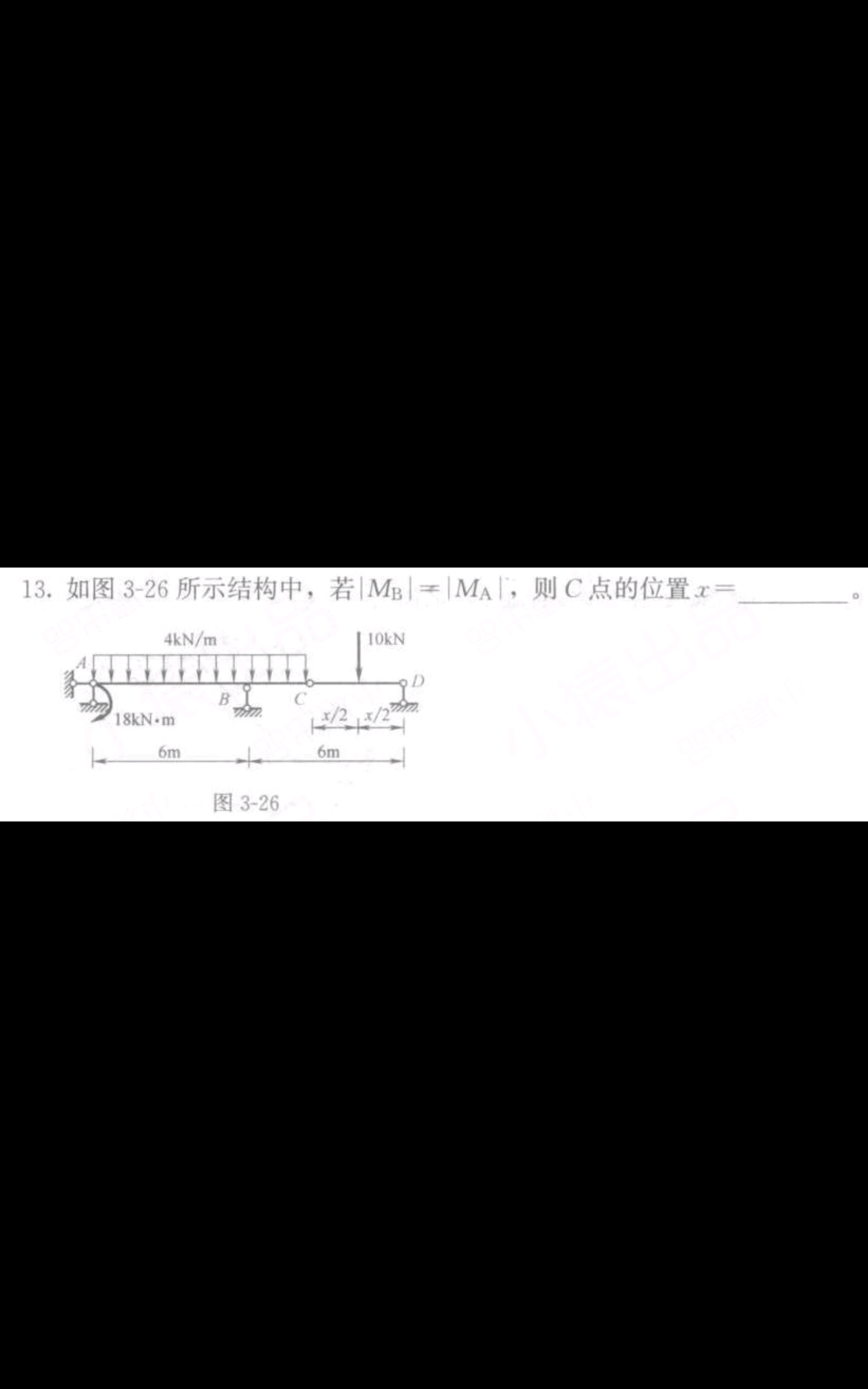
如图3-26所示结构中,若|MB|=|MA|,则C点的位置x=。
Understand the Problem
该问题要求我们确定在给定结构中点C的位置x,使得点B的弯矩|MB|等于点A的弯矩|MA|。需要使用力学原理和弯矩平衡来进行分析。
Answer
点C的位置为 $x = 3 \, \text{m}$。
Answer for screen readers
点C的位置 $x = 3 , \text{m}$。
Steps to Solve
- 计算点A的弯矩 $|M_A|$
计算点A的弯矩,假设点A处于右端。间隔为6米,施加的力为10kN。点A的弯矩公式为:
$$ |M_A| = 10 , \text{kN} \times 6 , \text{m} $$
- 计算点B的弯矩 $|M_B|$
将弯矩看作相对于点B的值,使用点C与点D之间的分布负载。分布负载为4kN/m,作用在6米之内。点C到点B的距离为$x$米,利用弯矩公式计算:
$$ |M_B| = \left(\frac{x}{2}\right) \times 4 , \text{kN/m} \times \left(6-x\right) $$
- 设置两个弯矩相等的方程
根据题目所述条件,我们设置方程:
$$ |M_B| = |M_A| $$
- 代入值并求解x
将$|M_A|$和$|M_B|$的表达式代入上述方程,并求解$x$:
$$ \left(\frac{x}{2}\right) \times 4 (6-x) = 60 , \text{kNm} $$
- 简化方程
将方程简化为:
$$ 2x(6-x) = 60 $$
- 解二次方程
将方程整理为标准形式,再求解$x$的值:
$$ x^2 - 6x + 30 = 0 $$
- 计算和验证解
使用求根公式计算$x$的值,确保得到的值满足题意。
点C的位置 $x = 3 , \text{m}$。
More Information
点C的位置是在整个结构中平衡弯矩相等的关键,这使得结构更容易管理和分配应力,从而提高稳定性。
Tips
- 在计算弯矩公式时,错将距离代入公式。
- 忽略了力的方向或作用点的位置。
- 在求解二次方程时出错,特别是在使用求根公式时。
AI-generated content may contain errors. Please verify critical information