2sin²θ + 5sinθ - 3 = 0
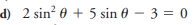
Understand the Problem
The question involves solving the trigonometric equation given as 2sin²θ + 5sinθ - 3 = 0. The goal is to find the values of θ that satisfy this equation.
Answer
$$\theta = \frac{\pi}{6} + 2k\pi \quad \text{and} \quad \theta = \frac{5\pi}{6} + 2k\pi \quad (k \in \mathbb{Z})$$
Answer for screen readers
The values of $\theta$ that satisfy the equation are: $$\theta = \frac{\pi}{6} + 2k\pi \quad \text{and} \quad \theta = \frac{5\pi}{6} + 2k\pi \quad (k \in \mathbb{Z})$$
Steps to Solve
-
Identify the quadratic form The equation $2\sin^2\theta + 5\sin\theta - 3 = 0$ is a quadratic in terms of $x = \sin\theta$.
-
Substitute and rearrange Let $x = \sin\theta$. The equation becomes: $$2x^2 + 5x - 3 = 0$$
-
Apply the quadratic formula To solve the quadratic equation, we use the quadratic formula: $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$ where $a = 2$, $b = 5$, and $c = -3$.
-
Calculate the discriminant First, calculate the discriminant: $$b^2 - 4ac = 5^2 - 4(2)(-3) = 25 + 24 = 49$$
-
Find the roots of the equation Substituting into the formula gives: $$x = \frac{-5 \pm \sqrt{49}}{2 \times 2} = \frac{-5 \pm 7}{4}$$
-
Calculate the two possible values of $x$ This results in:
- (x_1 = \frac{-5 + 7}{4} = \frac{2}{4} = \frac{1}{2})
- (x_2 = \frac{-5 - 7}{4} = \frac{-12}{4} = -3) (not valid since $\sin\theta$ must be in the range ([-1, 1]))
- Find values for $\theta$ Now we find $\theta$ when $\sin\theta = \frac{1}{2}$. The solutions are: $$\theta = \frac{\pi}{6} + 2k\pi \quad \text{and} \quad \theta = \frac{5\pi}{6} + 2k\pi$$ where $k \in \mathbb{Z}$.
The values of $\theta$ that satisfy the equation are: $$\theta = \frac{\pi}{6} + 2k\pi \quad \text{and} \quad \theta = \frac{5\pi}{6} + 2k\pi \quad (k \in \mathbb{Z})$$
More Information
The solutions $\theta = \frac{\pi}{6}$ and $\theta = \frac{5\pi}{6}$ correspond to angles where the sine function equals $\frac{1}{2}$. This is fundamental in trigonometry and can be visualized on the unit circle.
Tips
- Ignoring the range of sine values: Make sure not to accept values outside of the range ([-1, 1]) for $\sin\theta$.
- Not considering periodic nature: When finding solutions for trigonometric equations, always remember to add (2k\pi) for all integer values of (k).
AI-generated content may contain errors. Please verify critical information