√28 + √63
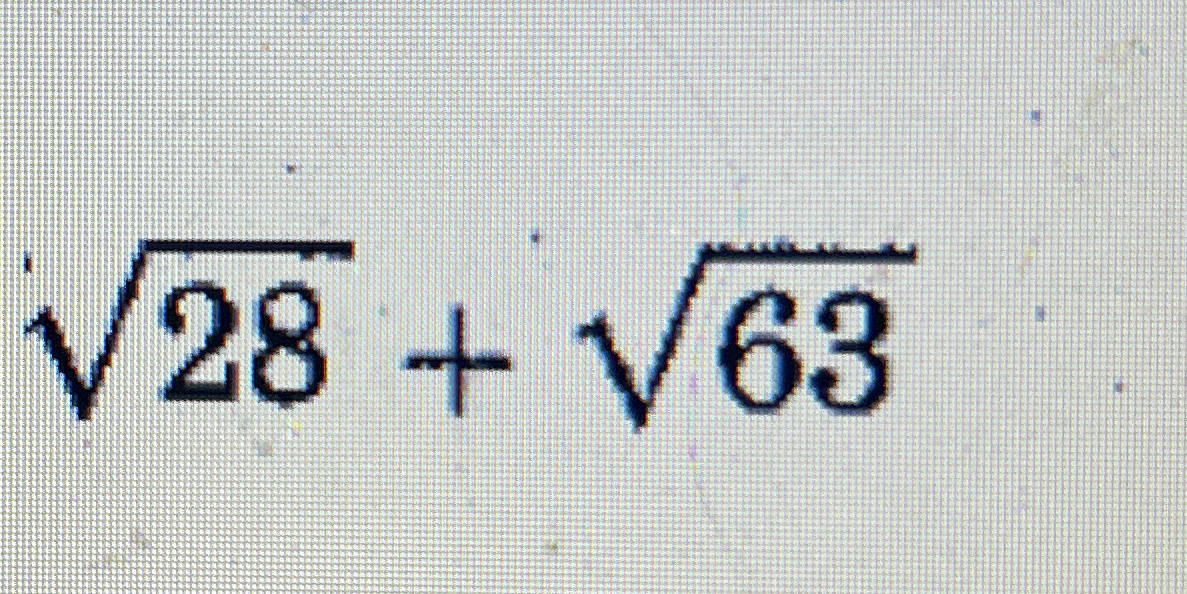
Understand the Problem
The question is asking to simplify the expression involving square roots of 28 and 63.
Answer
The simplified expression is \( 5\sqrt{7} \).
Answer for screen readers
The simplified expression is ( 5\sqrt{7} ).
Steps to Solve
-
Simplifying $\sqrt{28}$ To simplify $\sqrt{28}$, we can factor it into its prime components: $$ 28 = 4 \times 7 $$ Thus, $$ \sqrt{28} = \sqrt{4 \times 7} = \sqrt{4} \cdot \sqrt{7} = 2\sqrt{7} $$
-
Simplifying $\sqrt{63}$ Now we simplify $\sqrt{63}$. We factor 63 similarly: $$ 63 = 9 \times 7 $$ This gives us: $$ \sqrt{63} = \sqrt{9 \times 7} = \sqrt{9} \cdot \sqrt{7} = 3\sqrt{7} $$
-
Combining $\sqrt{28}$ and $\sqrt{63}$ Now, we can combine our simplifications: $$ \sqrt{28} + \sqrt{63} = 2\sqrt{7} + 3\sqrt{7} $$ Since both terms contain $\sqrt{7}$, we can add them: $$ (2 + 3)\sqrt{7} = 5\sqrt{7} $$
The simplified expression is ( 5\sqrt{7} ).
More Information
The result shows that both square roots could be combined by factoring out the common term, which is ( \sqrt{7} ). This technique is useful for simplifying expressions involving square roots.
Tips
- Not factoring completely: Some might forget to break down the numbers into their prime factors. Always look for the largest perfect squares.
- Overlooking like terms: When adding square roots, remember to combine coefficients of like radicals.
AI-generated content may contain errors. Please verify critical information