(-27) raised to the power of -1/3
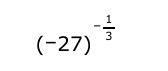
Understand the Problem
The question is asking to find the result of raising -27 to the power of -1/3, which involves understanding exponent rules, particularly with negative bases and fractional exponents.
Answer
$(-27)^{-1/3} = -\frac{1}{3}$
Answer for screen readers
The result of $(-27)^{-1/3}$ is $-\frac{1}{3}$.
Steps to Solve
-
Understanding the exponent The expression involves a negative exponent and a fractional exponent. The property of exponents states that $a^{-n} = \frac{1}{a^n}$, so we can rewrite the expression: $$ (-27)^{-1/3} = \frac{1}{(-27)^{1/3}} $$
-
Calculating the cube root Next, we need to calculate $(-27)^{1/3}$. The cube root of -27 is the number that, when multiplied by itself three times, equals -27. This number is -3, so we have: $$ (-27)^{1/3} = -3 $$
-
Putting it all together Now, substituting back into our rewritten expression, we get: $$ (-27)^{-1/3} = \frac{1}{(-3)} $$
-
Final calculation Finally, calculate the value: $$ (-27)^{-1/3} = -\frac{1}{3} $$
The result of $(-27)^{-1/3}$ is $-\frac{1}{3}$.
More Information
Negative bases raised to a fractional exponent can yield real numbers, provided the root denominator is odd, as the cube root allows for negative outcomes.
Tips
- Confusing the negative exponent: Remember that a negative exponent indicates a reciprocal, which can sometimes be confused with just taking the negative of the base.
- Miscalculating roots: Ensure you correctly evaluate roots of negative numbers, especially when the root is odd.
AI-generated content may contain errors. Please verify critical information