√(25 * 3)
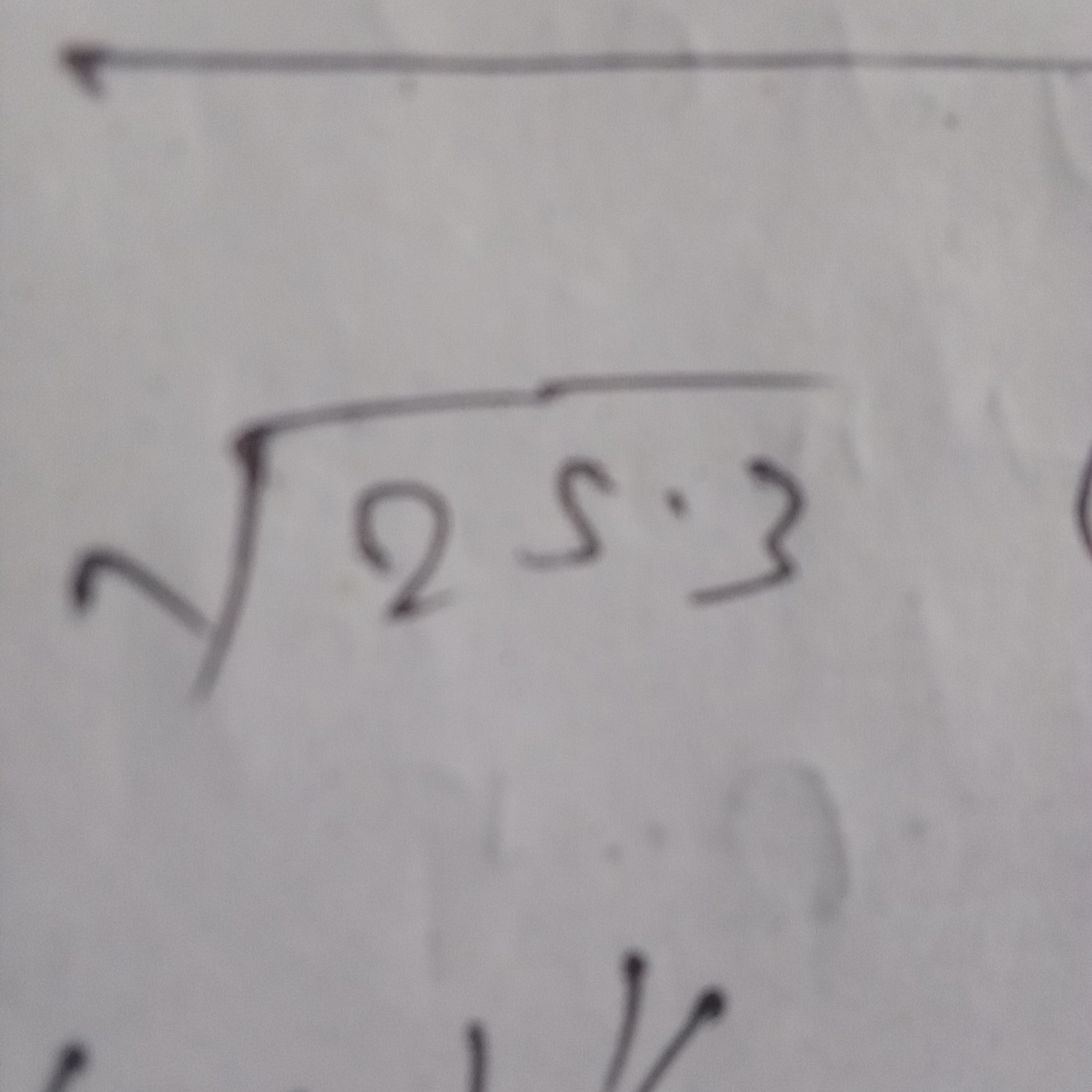
Understand the Problem
The question involves calculating the square root of the product of 25 and 3. We will use the property of square roots to simplify this expression.
Answer
The answer is \( 5\sqrt{3} \).
Answer for screen readers
The final answer is ( 5\sqrt{3} ).
Steps to Solve
- Calculate the Product Inside the Square Root
First, calculate the product of 25 and 3:
$$ 25 \times 3 = 75 $$
- Take the Square Root of the Product
Now, find the square root of the product:
$$ \sqrt{75} $$
- Simplify the Square Root
To simplify, we can factor 75 into its prime factors:
$$ 75 = 25 \times 3 = 5^2 \times 3 $$
Thus, the square root can be expressed as:
$$ \sqrt{75} = \sqrt{25 \times 3} = \sqrt{25} \times \sqrt{3} $$
- Calculate the Square Root of 25
The square root of 25 is:
$$ \sqrt{25} = 5 $$
- Combine the Results
Putting it all together, we have:
$$ \sqrt{75} = 5 \times \sqrt{3} $$
The final answer is ( 5\sqrt{3} ).
More Information
Expressing square roots in simplified form can help clarify results in mathematics. The number ( 5\sqrt{3} ) is an exact expression showing both the integer and the irrational part, which is often a preferable way to present an answer.
Tips
- Forgetting to simplify the square root: It's common to leave the square root unsimplified.
- Incorrectly calculating the product of the numbers: Ensure that multiplication is performed correctly before taking the square root.
AI-generated content may contain errors. Please verify critical information