(-2)³ + 5²

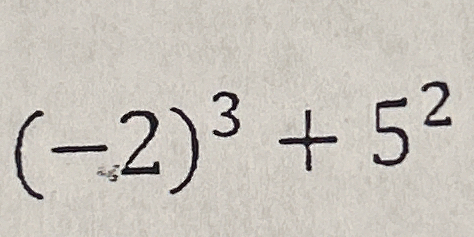
Understand the Problem

The question is asking us to evaluate the expression (-2)^3 + 5^2, which involves calculating the cube of negative two and the square of five, then adding the two results together.

Answer

$17$

Steps to Solve

Calculate $(-2)^3$

To find $(-2)^3$, multiply -2 by itself three times:

$$ (-2)^3 = (-2) \times (-2) \times (-2) = 4 \times (-2) = -8 $$

Calculate $5^2$

Now, compute $5^2$, which is 5 multiplied by itself:

$$ 5^2 = 5 \times 5 = 25 $$

Add the results

Combine the two results obtained in the previous steps:

$$ (-2)^3 + 5^2 = -8 + 25 $$

Final Result

Now simplify:

$$ -8 + 25 = 17 $$

The final answer is $17$.

More Information

The expression combines powers of negative and positive numbers. Evaluating each part separately helps ensure accuracy. The cube of a negative number will always be negative, while the square of a positive number is positive.

Tips

Not applying the negative sign correctly: Remember that cubing a negative number results in a negative value.
Confusing operations: Ensure multiplication and exponentiation are executed correctly to avoid simple arithmetic errors.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!