-21/28 ÷ (-7/4)
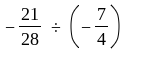
Understand the Problem
The question involves performing operations on fractions, specifically division of one fraction by another. We will need to simplify and find the final result of the expression.
Answer
The final answer is $\frac{3}{7}$.
Answer for screen readers
The final answer is $\frac{3}{7}$.
Steps to Solve
-
Rewrite the division as multiplication To divide by a fraction, we multiply by its reciprocal. Therefore, we can rewrite the expression: $$ -\frac{21}{28} \div -\frac{7}{4} = -\frac{21}{28} \times -\frac{4}{7} $$
-
Multiply the fractions Next, we multiply the two fractions: $$ -\frac{21 \times 4}{28 \times 7} $$
-
Compute the numerator and denominator Calculate the values in the numerator and denominator:
- Numerator: ( 21 \times 4 = 84 )
- Denominator: ( 28 \times 7 = 196 )
So, the expression now looks like: $$ \frac{84}{196} $$
- Simplify the fraction We can simplify ( \frac{84}{196} ) by finding the greatest common divisor (GCD) of 84 and 196, which is 28: $$ \frac{84 \div 28}{196 \div 28} = \frac{3}{7} $$
The final answer is $\frac{3}{7}$.
More Information
The division of fractions involves multiplying by the reciprocal, which simplifies calculations. Understanding how to simplify fractions can lead to quicker solutions.
Tips
- Not converting division to multiplication: Some may forget to take the reciprocal of the second fraction.
- Incorrect simplification: It’s important to find the correct GCD when simplifying fractions to avoid errors.
AI-generated content may contain errors. Please verify critical information