20x - 2(x + 10) = -(5 - 2x)
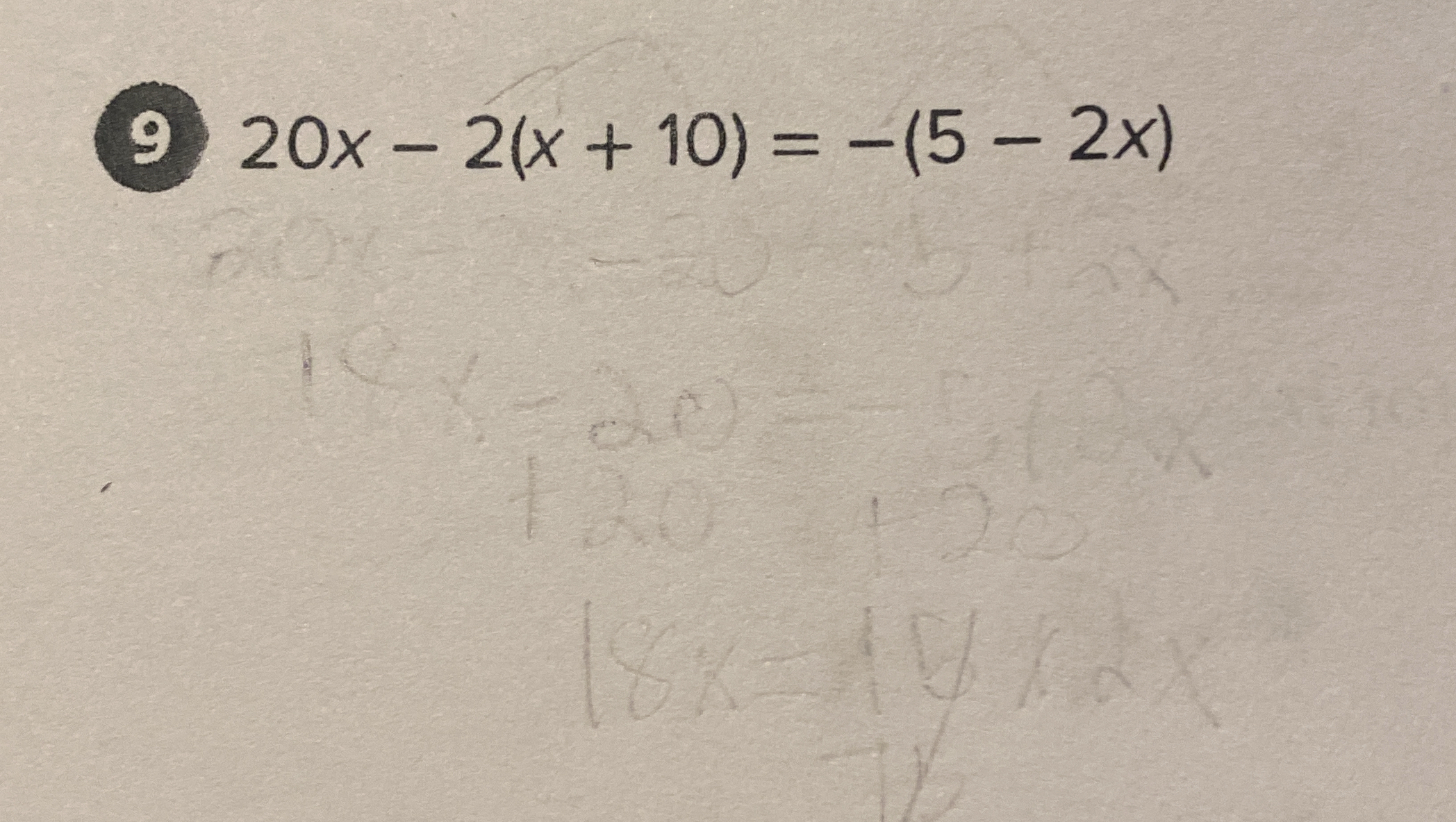
Understand the Problem
The question is asking to solve the equation given, which involves distributing and combining like terms to find the value of x.
Answer
The solution is $x = \frac{15}{16}$.
Answer for screen readers
The value of $x$ is $x = \frac{15}{16}$.
Steps to Solve
- Distribute the terms inside the parentheses
We first distribute $-2$ across $(x + 10)$ and $-(5 - 2x)$ across the entire right side of the equation:
$$ 20x - 2(x + 10) = -(5 - 2x) $$
This becomes:
$$ 20x - 2x - 20 = -5 + 2x $$
- Combine like terms
Next, we combine the like terms on the left side:
$$ (20x - 2x) - 20 = -5 + 2x $$
This simplifies to:
$$ 18x - 20 = -5 + 2x $$
- Move all terms involving x to one side
To isolate $x$, we can move $2x$ from the right side to the left side by subtracting $2x$ from both sides:
$$ 18x - 2x - 20 = -5 $$
This simplifies to:
$$ 16x - 20 = -5 $$
- Add 20 to both sides
We add 20 to both sides of the equation to isolate the term with $x$:
$$ 16x - 20 + 20 = -5 + 20 $$
This leads to:
$$ 16x = 15 $$
- Divide both sides by 16
Finally, we solve for $x$ by dividing both sides by 16:
$$ x = \frac{15}{16} $$
The value of $x$ is $x = \frac{15}{16}$.
More Information
This equation involves distributing, combining like terms, and isolating the variable in a linear equation format.
Tips
- Neglecting to distribute the negative signs correctly, leading to incorrect terms.
- Forgetting to combine like terms properly.
- Not isolating $x$ correctly by combining or moving all terms involving $x$ to one side.
AI-generated content may contain errors. Please verify critical information