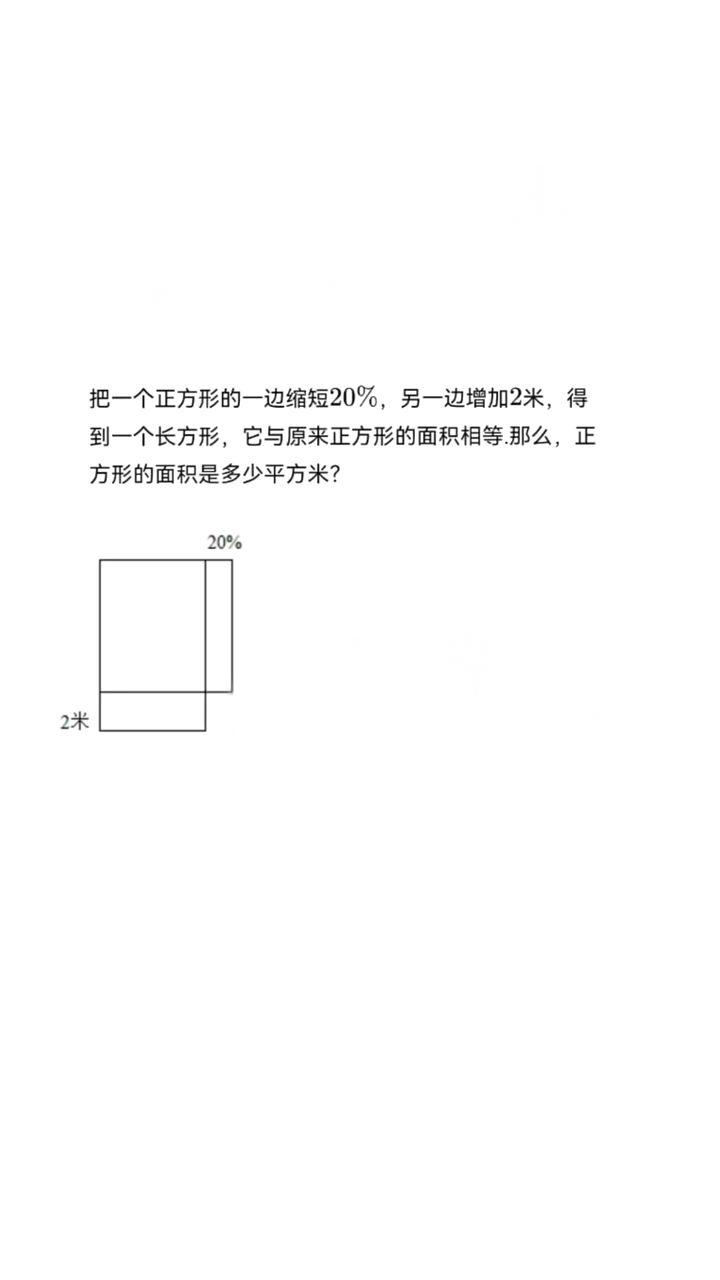
把一个正方形的一边缩短20%，另一边增加2米，得到一个长方形，它与原来正方形的面积相等。那么，正方形的面积是多少平方米？

Steps to Solve

1. 设定变量 设定原正方形的边长为 $x$ 米。那么，原正方形的面积 $A$ 为： $$ A = x^2 $$

2. 计算缩短后的边长 一边缩短20%，所以新的边长为： $$ x - 0.2x = 0.8x $$

3. 计算增加后的边长 另一边增加2米，新的边长为： $$ x + 2 $$

4. 设定等式 新的长方形面积与原正方形面积相等，所以： $$ 0.8x \cdot (x + 2) = x^2 $$

5. 简化等式 展开等式并简化： $$ 0.8x^2 + 1.6x = x^2 $$

6. 移项整理 将所有项移到一边，得到： $$ 0 = x^2 - 0.8x^2 - 1.6x $$ $$ 0 = 0.2x^2 - 1.6x $$

7. 因式分解 提取公因数： $$ 0 = 0.2x(x - 8) $$

8. 求解方程 得到两个解： $$ x = 0 \text{ 或 } x = 8 $$

9. 计算面积 由于边长不能为0，取 $x = 8$，因此原正方形的面积为： $$ A = 8^2 = 64 $$