[2001] [0 2 1]^T [5 1 6] = ( )
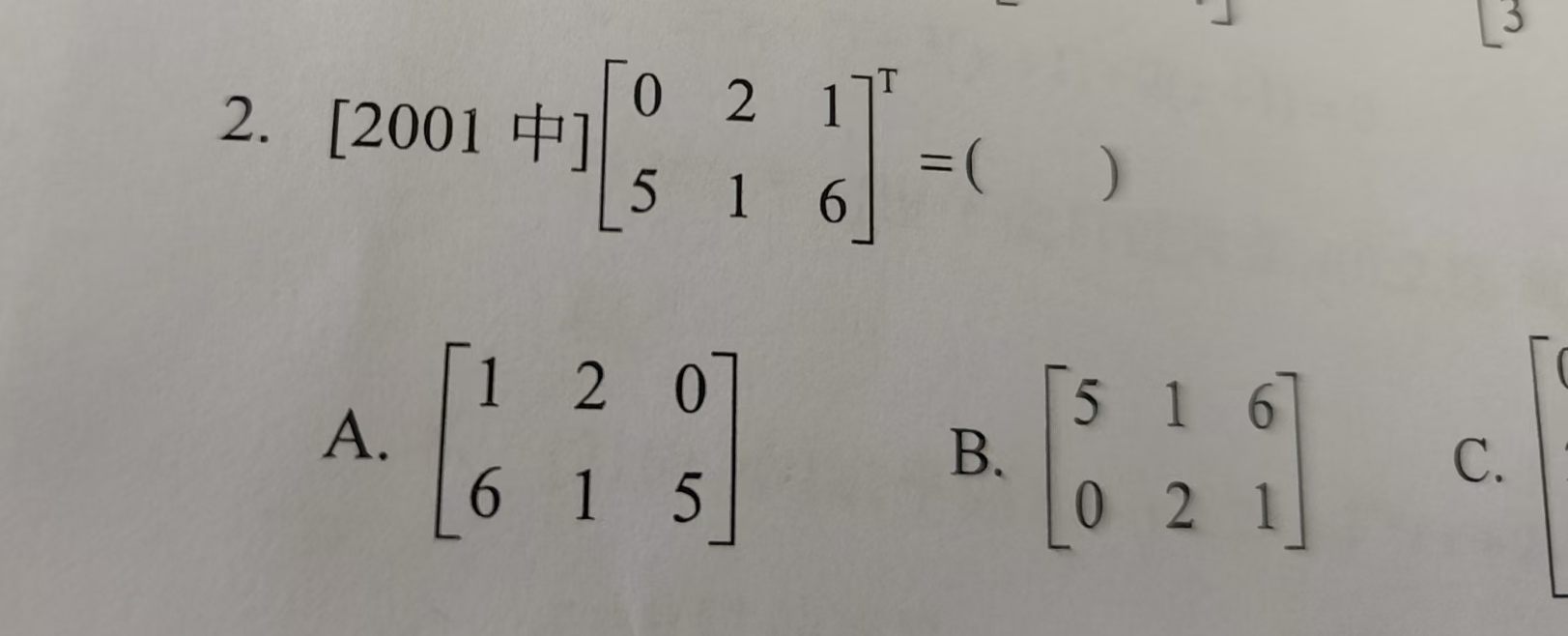
Understand the Problem
The question is asking to perform matrix multiplication with the given matrices and then match the result to one of the provided options.
Answer
The resulting matrix is $$ \begin{bmatrix} 10 \\ 2 \\ 41 \end{bmatrix} $$
Answer for screen readers
The final answer is: $$ \begin{bmatrix} 10 \ 2 \ 41 \end{bmatrix} $$
Steps to Solve
-
Identify the matrices The matrices given are: $$ A = \begin{bmatrix} 2 & 0 \ 0 & 2 \ 1 & 6 \end{bmatrix}, \quad B = \begin{bmatrix} 5 \ 1 \ 6 \end{bmatrix} $$
-
Determine the dimensions Matrix A is a (3 \times 2) matrix and matrix B is a (3 \times 1) vector.
-
Matrix multiplication setup To find the product ( AB ), we need to ensure the inner dimensions match. Since A has (2) columns and B has (3) rows, we can't multiply them directly.
-
Transpose matrix B Transposing B gives us a (1 \times 3) matrix: $$ B^T = \begin{bmatrix} 5 & 1 & 6 \end{bmatrix} $$
-
Perform the multiplication Now, multiply matrix A by the transposed matrix B: $$ AB^T = \begin{bmatrix} 2 & 0 \ 0 & 2 \ 1 & 6 \end{bmatrix} \begin{bmatrix} 5 \ 1 \ 6 \end{bmatrix} $$
-
Calculate each entry of the resulting matrix For each element in the resulting matrix:
- First row: ( (2 \cdot 5) + (0 \cdot 1) + (0 \cdot 6) = 10 )
- Second row: ( (0 \cdot 5) + (2 \cdot 1) + (0 \cdot 6) = 2 )
- Third row: ( (1 \cdot 5) + (0 \cdot 1) + (6 \cdot 6) = 5 + 0 + 36 = 41 )
- Form the result matrix The resulting matrix after multiplication is: $$ \begin{bmatrix} 10 \ 2 \ 41 \end{bmatrix} $$
The final answer is: $$ \begin{bmatrix} 10 \ 2 \ 41 \end{bmatrix} $$
More Information
The calculations demonstrate how matrix multiplication can be performed step by step. In this case, the result matrix is a column vector representing the combined linear transformations defined by matrices A and B.
Tips
- Forgetting to transpose a matrix when required for multiplication.
- Not ensuring the dimensions of the matrices are compatible for multiplication before proceeding.
AI-generated content may contain errors. Please verify critical information