(-2) × 5 × 8 × (-4)

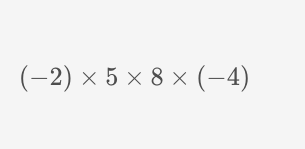
Understand the Problem

The question is asking us to calculate the product of the numbers given in the expression, which involves multiplication of negative and positive integers.

Answer

$320$

Steps to Solve

Identify the Signs of the Numbers

The numbers in the expression are:

Negative: $-2$ and $-4$
Positive: $5$ and $8$

Count the Negative Numbers

In this expression, there are two negative numbers ($-2$ and $-4$). Since the product of two negative numbers is positive, the result of multiplying these will be positive.

Multiply the Positive and Negative Values

First, multiply the absolute values of all the numbers: $$ |(-2)| \times |5| \times |8| \times |(-4)| = 2 \times 5 \times 8 \times 4 $$

Calculating step by step:

Multiply $2$ and $5$: $$ 2 \times 5 = 10 $$
Then multiply the result by $8$: $$ 10 \times 8 = 80 $$
Finally, multiply by $4$: $$ 80 \times 4 = 320 $$

Determine the Final Sign

Since we have multiplied two negative numbers together, the result will be positive. Therefore, the final result is: $$ 320 $$

The final answer is $320$.

More Information

The multiplication of negative and positive integers follows specific rules: a negative times a positive is negative, and a negative times a negative is positive. This example highlights how two negatives result in a positive product.

Tips

Forgetting to multiply the negative signs correctly. Remember that two negatives will always make a positive.
Not keeping track of the signs during calculation. Always check the sign of the final product based on the number of negatives.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!