-1/3 - ( -8/7 )
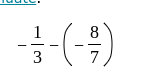
Understand the Problem
The question is asking us to simplify the expression containing fractions. This involves operations with fractions, such as finding a common denominator and performing the necessary calculations.
Answer
The simplified expression is $$ \frac{17}{21} $$.
Answer for screen readers
The final simplified expression is $$ \frac{17}{21} $$.
Steps to Solve
-
Rewrite the expression
We start with the expression: $$ -\frac{1}{3} - \left( -\frac{8}{7} \right) $$ This can be rewritten as: $$ -\frac{1}{3} + \frac{8}{7} $$
-
Find a common denominator
The denominators are 3 and 7. The least common denominator (LCD) is 21.
-
Convert fractions to have a common denominator
Convert $-\frac{1}{3}$ and $\frac{8}{7}$ to have the denominator of 21: $$ -\frac{1}{3} = -\frac{1 \times 7}{3 \times 7} = -\frac{7}{21} $$ $$ \frac{8}{7} = \frac{8 \times 3}{7 \times 3} = \frac{24}{21} $$
-
Combine the fractions
Now we can combine the fractions: $$ -\frac{7}{21} + \frac{24}{21} = \frac{-7 + 24}{21} = \frac{17}{21} $$
-
Final result
The simplified expression is: $$ \frac{17}{21} $$
The final simplified expression is $$ \frac{17}{21} $$.
More Information
The simplification shows how operations with fractions work, particularly focusing on finding a common denominator. This is a key skill in fraction arithmetic.
Tips
- Neglecting the negative sign: When converting the negative fraction, ensure the sign is correctly applied throughout the process.
- Incorrect LCD calculation: Always double-check the least common denominator, as this is crucial for fraction addition and subtraction.
AI-generated content may contain errors. Please verify critical information