√(12x) * √(3x)
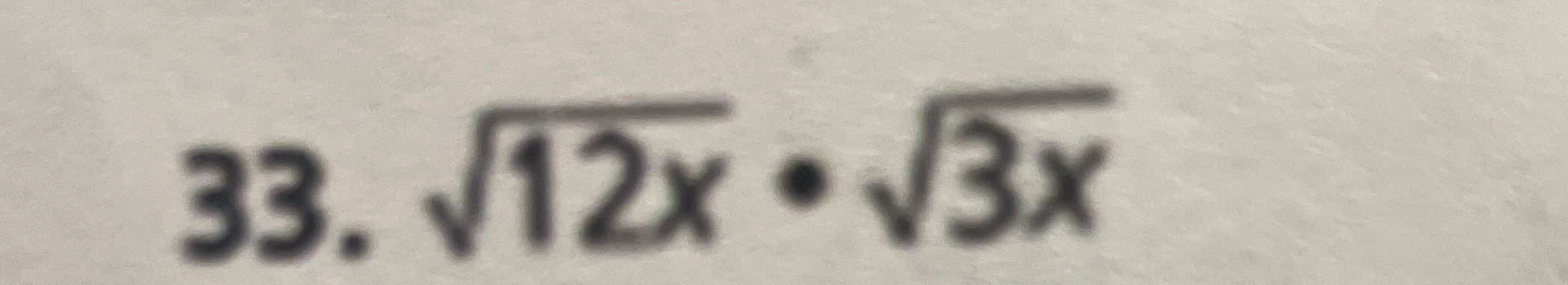
Understand the Problem
The question involves simplifying the expression involving square roots of products of variables. We need to simplify the expression √(12x) * √(3x).
Answer
$6x$
Answer for screen readers
The final simplified answer is $6x$.
Steps to Solve
-
Combine the Square Roots We can combine the two square root expressions using the property that $\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}$. Thus, we have: $$ \sqrt{12x} \cdot \sqrt{3x} = \sqrt{(12x) \cdot (3x)} $$
-
Multiply Inside the Square Root Now, we need to multiply the expressions inside the square root: $$ (12x) \cdot (3x) = 36x^2 $$
-
Simplify the Square Root Now, we can simplify the square root of the product: $$ \sqrt{36x^2} = \sqrt{36} \cdot \sqrt{x^2} $$
-
Calculate the Square Roots We know that $\sqrt{36} = 6$ and $\sqrt{x^2} = x$, so combining these gives us: $$ \sqrt{36x^2} = 6x $$
The final simplified answer is $6x$.
More Information
When simplifying square root expressions, combining and multiplying under one square root can greatly reduce complexity. In this case, we used the property of square roots effectively to find a neatly simplified expression.
Tips
- Forgetting to combine the square roots before multiplying can lead to more complicated expressions.
- Not simplifying the final square root correctly can result in an incorrect final answer.
AI-generated content may contain errors. Please verify critical information