(-1/2 + x)(a - 8)
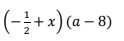
Understand the Problem
The question is presenting a mathematical expression involving variables and constants. The task may require simplifying or evaluating the expression based on certain values.
Answer
The simplified expression is $xa - \frac{1}{2}a - 8x + 4$.
Answer for screen readers
The simplified expression is:
$$ xa - \frac{1}{2}a - 8x + 4 $$
Steps to Solve
- Distribute the first term We start by multiplying each term in the first expression $(-\frac{1}{2} + x)$ by the second expression $(a - 8)$.
$$ (-\frac{1}{2})(a - 8) + x(a - 8) $$
- Distribute $-\frac{1}{2}$ Now, distribute $-\frac{1}{2}$ across $a - 8$.
$$ -\frac{1}{2}a + 4 $$
- Distribute $x$ Next, distribute $x$ across $a - 8$.
$$ xa - 8x $$
- Combine the results Now combine both results from the previous distributions:
$$ -\frac{1}{2}a + 4 + xa - 8x $$
- Rearrange the expression You may rearrange the terms for clarity:
$$ xa - \frac{1}{2}a - 8x + 4 $$
The simplified expression is:
$$ xa - \frac{1}{2}a - 8x + 4 $$
More Information
This expression represents the product of a binomial and a monomial, and highlights how distribution works in algebra, allowing us to combine like terms effectively.
Tips
- Incorrectly applying the distributive property: Make sure to distribute each term individually.
- Forgetting to combine like terms: Always check if there are similar terms that can be combined at the end.
AI-generated content may contain errors. Please verify critical information