11xy^{-1}-1z^{0} / v^{-3}
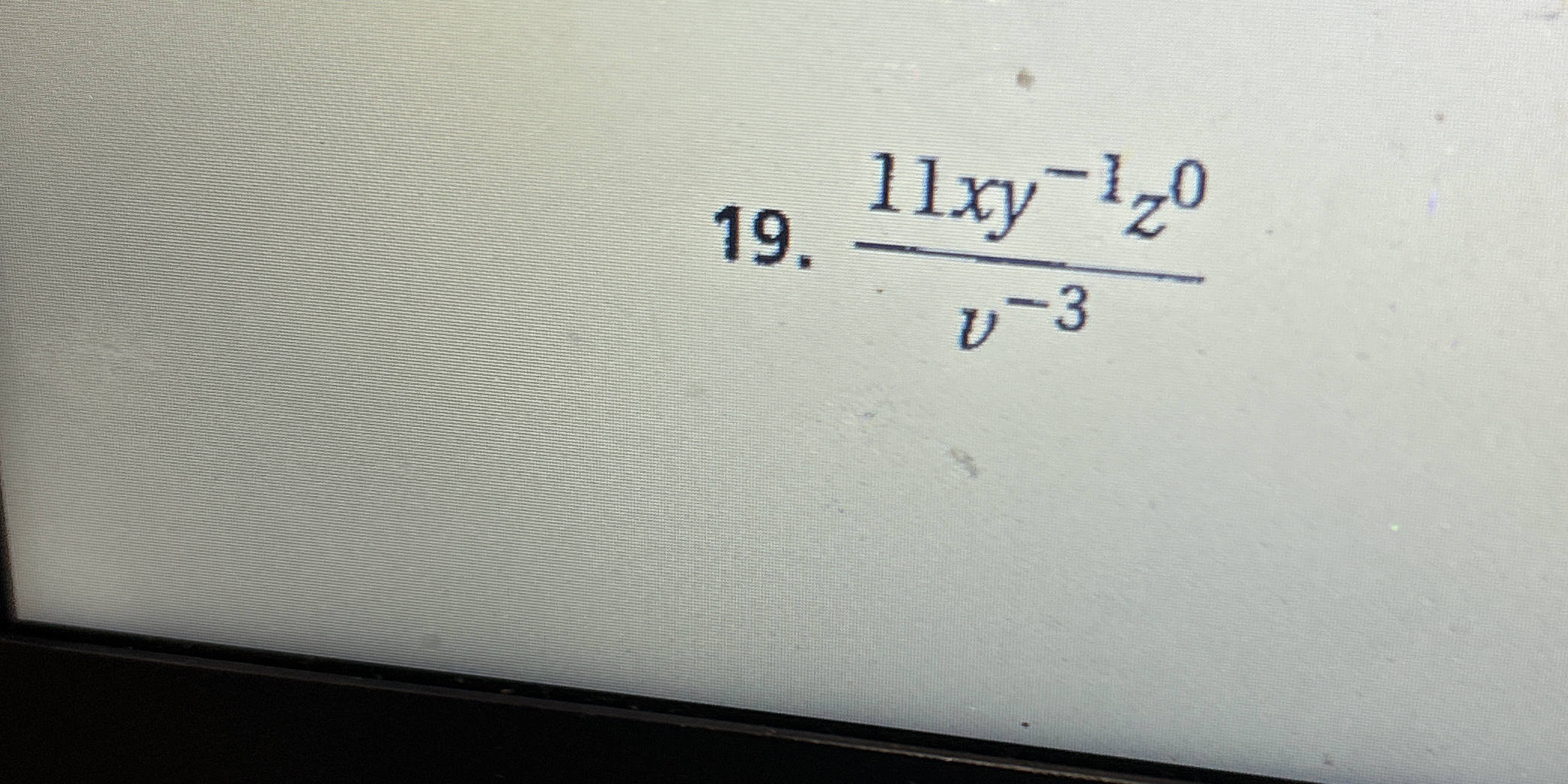
Understand the Problem
The question presents a mathematical expression that involves variables and a fraction. It is likely asking for some manipulation, evaluation, or simplification of the expression. The context and specific instructions on what to do with the expression are not provided in the image.
Answer
The final simplified expression is $$ 11xy^{3} - v^{3} $$.
Answer for screen readers
The simplified expression is:
$$ 11xy^{3} - v^{3} $$
Steps to Solve
- Identify the terms in the expression
The expression is given as:
$$ \frac{11xy^{-1} - 1z^{0}}{v^{-3}} $$
Identify each term:
- The numerator consists of $11xy^{-1} - 1z^{0}$.
- The denominator is $v^{-3}$.
- Simplify the term $z^{0}$
Using the property of exponents, $z^{0} = 1$.
So, the expression can now be rewritten as:
$$ \frac{11xy^{-1} - 1}{v^{-3}} $$
- Rewrite the negative exponent
Recall that $v^{-3} = \frac{1}{v^3}$. Therefore, the denominator can be rewritten to eliminate the negative exponent:
$$ \frac{11xy^{-1} - 1}{\frac{1}{v^{3}}} $$
- Multiply by the reciprocal
To simplify the fraction, multiply by the reciprocal of the denominator:
$$ (11xy^{-1} - 1) \cdot v^{3} $$
- Distribute $v^{3}$ into the terms in the parentheses
The expression becomes:
$$ 11xy^{-1} v^{3} - v^{3} $$
Final simplified expression:
$$ 11 \frac{xy^{3}}{1} - v^{3} $$
The simplified expression is:
$$ 11xy^{3} - v^{3} $$
More Information
This simplification uses properties of exponents, particularly how negative exponents and zero exponents function. Understanding these properties can make manipulating expressions easier in algebra.
Tips
- Ignoring $z^{0}$: Remember that any non-zero number raised to the power of zero equals 1.
- Confusing negative exponents: Misunderstanding that $v^{-3} = \frac{1}{v^3}$ can lead to mistakes in the simplification process.
AI-generated content may contain errors. Please verify critical information