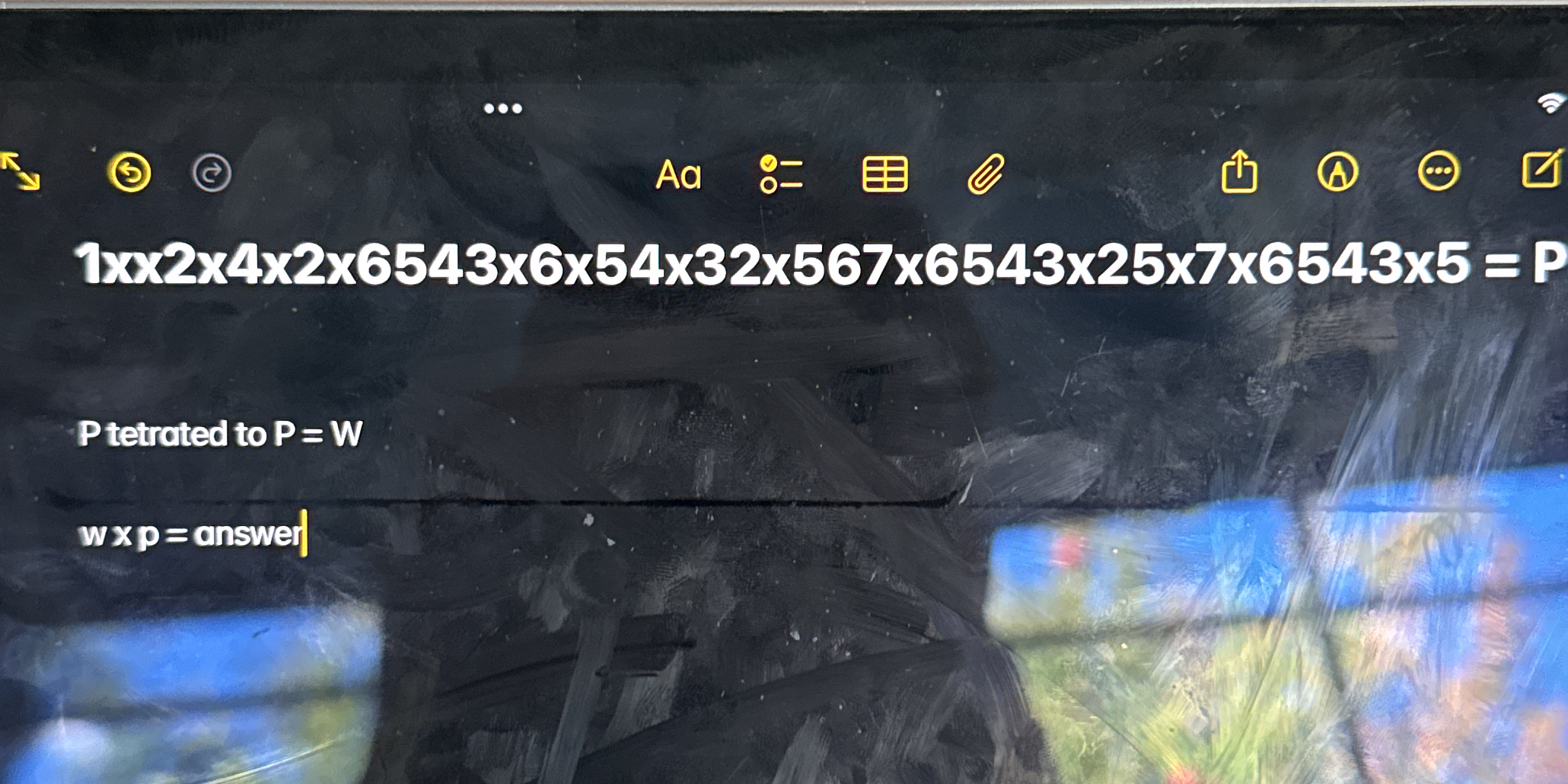
1 xx 2 x 4 x 2 x 6543 x 6 x 54 x 32 x 567 x 6543 x 25 x 7 x 6543 x 5 = P; P tetrated to P = W; w x p = answer
Understand the Problem
The question appears to involve a mathematical expression involving a series of multiplications, a variable P that is equated to W, and an expression involving 'w x p'. The goal seems to involve calculating or simplifying these expressions.
Answer
To calculate the answer, we need \( P \), \( W = P \uparrow\uparrow P \), and \( \text{answer} = w \times P \). The exact values are impractical to compute without a calculator.
Answer for screen readers
The value of ( P ) must be calculated directly, and ( W ) and the final answer cannot be computed without knowing ( w ). Specifically:
- ( P ) can be found by calculating all the products.
- ( W = P \uparrow\uparrow P ).
- ( \text{answer} = w \times P ).
Steps to Solve
- Calculate the Product P
First, we need to calculate the product of all the numbers given:
$$ P = 1 \times 2 \times 4 \times 2 \times 6543 \times 6 \times 54 \times 32 \times 567 \times 6543 \times 25 \times 7 \times 6543 \times 5 $$
This can be computed step by step, but it's advisable to use a calculator or programming language for efficiency due to the large numbers.
- Tetrate P to Get W
Next, we want to evaluate ( P ) tetrated to ( P ), denoted as ( P \uparrow\uparrow P ). Tetration is essentially exponentiation repeated. This would look like:
$$ W = P^P^P \cdots \text{(P times)} $$
Calculating actual values here becomes infeasible for large ( P ), but you can note it as ( W = P \uparrow\uparrow P ).
- Calculate w x p
Assuming ( w ) is given or can be calculated, we need to multiply ( w ) and ( p ):
$$ \text{answer} = w \times P $$
Again, this step would depend on the value of ( w ).
The value of ( P ) must be calculated directly, and ( W ) and the final answer cannot be computed without knowing ( w ). Specifically:
- ( P ) can be found by calculating all the products.
- ( W = P \uparrow\uparrow P ).
- ( \text{answer} = w \times P ).
More Information
Calculating such a large product and tetration results in very large numbers. It’s impractical to compute beyond simple multiplication within normal calculators. Tetration grows extremely fast, much faster than regular exponentiation.
Tips
- Forgetting Order of Operations: Ensure to multiply all terms in the correct order.
- Misunderstanding Tetration: Tetration is not the same as repeated multiplication; make sure to clearly define what ( P \uparrow\uparrow P ) means.
- Overlooking the Scale of Numbers: Realize that numbers can get extremely large quickly and might exceed computational capabilities.
AI-generated content may contain errors. Please verify critical information