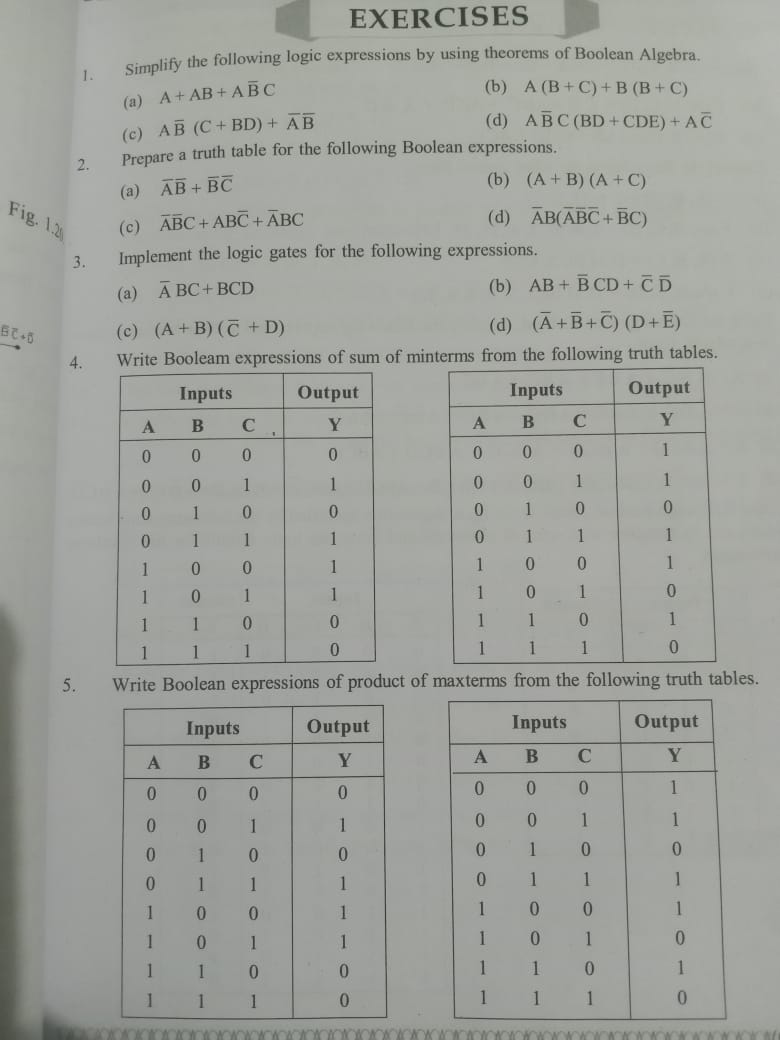
1. Simplify the following logic expressions using theorems of Boolean Algebra: (a) A + AB + ABC (b) A(B + C) + B(B + C) (c) AB(C + BD) + AB (d) ABC(BD + CDE) + AC 2. Prepare a trut... 1. Simplify the following logic expressions using theorems of Boolean Algebra: (a) A + AB + ABC (b) A(B + C) + B(B + C) (c) AB(C + BD) + AB (d) ABC(BD + CDE) + AC 2. Prepare a truth table for the following Boolean expressions: (a) AB + BC (b) (A + B)(A + C) (c) ABC + ABC + ABC 3. Implement the logic gates for the following expressions: (a) ABC + BCD (b) AB + BCD + CD (c) (A + B)(C + D) (d) (A + B + C)(D + E) 4. Write Boolean expressions of sum of minterms from the following truth tables. 5. Write Boolean expressions of product of maxterms from the following truth tables.
Understand the Problem
The question is asking to simplify Boolean logic expressions, prepare truth tables for specific expressions, implement logic gates for given expressions, and write Boolean expressions from provided truth tables.
Answer
(a) $A$ (b) $(A + B)(B + C)$ (c) $A(\overline{B} + \overline{C}) + \overline{A}BC$ (d) $BC(A(D + DE) + \overline{A})$
Answer for screen readers
-
(a) $A$
(b) $(A + B)(B + C)$
(c) $A(\overline{B} + \overline{C}) + \overline{A}BC$
(d) $BC(A(D + DE) + \overline{A})$ -
Truth tables ready for evaluation based on Boolean expressions.
-
Logic gates implemented based on given expressions.
-
Minterm and maxterm expressions from truth tables created.
Steps to Solve
- Simplifying Boolean Expressions (1a)
Starting with the expression $A + AB + ABC$. We can apply the Absorption Law: $A + AB = A$. Thus, we have:
$$ A + AB + ABC = A + ABC = A $$
- Continuing with Simplifications (1b)
For the expression $A(B + C) + B(B + C)$, we can factor out $(B + C)$:
$$ A(B + C) + B(B + C) = (A + B)(B + C) $$
- Simplifying Expression (1c)
For $A \overline{B} + A \overline{C} + \overline{A} B C$, we can factor out $A$ from the first two terms:
$$ A(\overline{B} + \overline{C}) + \overline{A} B C $$
- Finalizing Simplifications (1d)
The expression is $ABC(BD + CDE) + \overline{A}C$. Here we can factor $BC$:
$$ BC(A(D + DE) + \overline{A}) $$
- Preparing a Truth Table (2a)
For the expression $A \overline{B} + \overline{B} C$, we create the truth table with combinations of A, B, and C. List all combinations (000 to 111) and evaluate.
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
- Truth Table for Expression (2b)
For $(A + B)(A + C)$, continue the truth table similarly and evaluate:
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
- Truth Table for Another Expression (2c)
For $ABC + ABC$, the truth table will have similar steps as above.
- Implementing Logic Gates (3a)
The expression $A \overline{B} C + BCD$ can be implemented using AND, OR, and NOT gates. Construct the logic circuit.
- Continuing Logic Gates Implementation (3b)
Implementing $AB + \overline{B} CD + \overline{C} \overline{D}$ similarly using gates.
- Writing Minterms and Maxterms (Questions 4 & 5)
Identify positions in the truth tables for 1s (for minterms) and 0s (for maxterms) and write down the respective expressions.
-
(a) $A$
(b) $(A + B)(B + C)$
(c) $A(\overline{B} + \overline{C}) + \overline{A}BC$
(d) $BC(A(D + DE) + \overline{A})$ -
Truth tables ready for evaluation based on Boolean expressions.
-
Logic gates implemented based on given expressions.
-
Minterm and maxterm expressions from truth tables created.
More Information
Simplification of Boolean expressions can reduce circuit complexity. Truth tables provide a methodical way to evaluate the outcomes of logic functions. Logic gates physically realize these Boolean expressions in hardware.
Tips
- Not applying the Absorption Law correctly.
- Confusing AND with OR operations in truth tables.
- Errors in evaluating logic gate outputs.
AI-generated content may contain errors. Please verify critical information