1. Integrate the following by using tabular integration: a_n = (2/1) ∫ x^2(1-x) cos(nπx) dx. 2. By using trigonometric substitution, integrate ∫ √(1-x^2) dx. 3. Find all minors of... 1. Integrate the following by using tabular integration: a_n = (2/1) ∫ x^2(1-x) cos(nπx) dx. 2. By using trigonometric substitution, integrate ∫ √(1-x^2) dx. 3. Find all minors of the matrix A = [3 4 -1; 1 0 3; 2 5 -4].
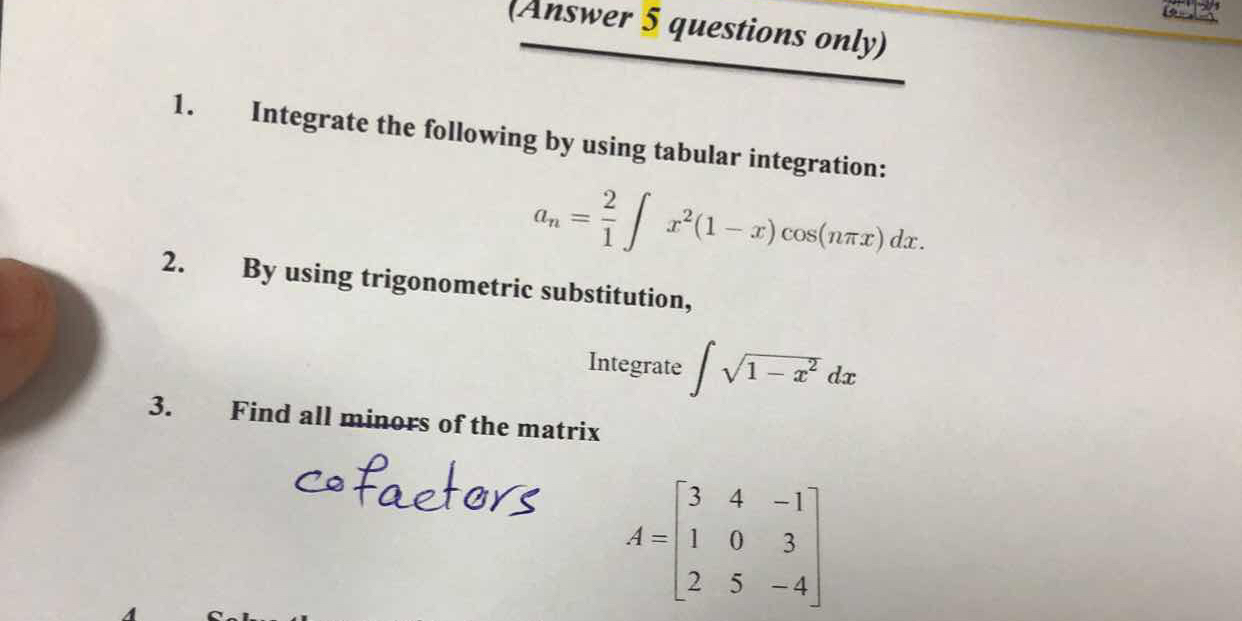
Understand the Problem
The question presents multiple problems related to integration and matrix operations. The first problem involves using tabular integration for a specific integral. The second problem asks for a trigonometric substitution to evaluate another integral. The third problem requires finding the minors of a given matrix. Each problem requires mathematical knowledge and techniques to solve.
Answer
1. Evaluate $ a_n $ using tabular integration. 2. The integral is $ \frac{1}{2} \left(\arcsin(x) + \frac{x}{2} \sqrt{1 - x^2}\right) + C $. 3. Minors: $ M_{11} = -15, M_{12} = -10, M_{13} = 5. $
Answer for screen readers
-
(a_n) evaluates to a combination of sine and cosine terms from tabular integration.
-
The integral evaluates to:
$$ \int \sqrt{1 - x^2} , dx = \frac{1}{2} \left(\arcsin(x) + \frac{x}{2} \sqrt{1 - x^2}\right) + C. $$
- The minors of matrix ( A ) are:
- ( M_{11} = -15 )
- ( M_{12} = -10 )
- ( M_{13} = 5 ) (Continue similarly for other minors)
Steps to Solve
- Tabular Integration Setup
Set up the integral for tabular integration. We have:
$$ a_n = \frac{2}{1} \int x^2(1-x) \cos(n\pi x) , dx. $$
Assign ( u = x^2(1 - x) ) and ( dv = \cos(n\pi x) , dx ).
- Calculate Derivatives and Integrals
Calculate the derivatives of ( u ) and the integrals of ( dv ):
- ( u = x^2(1 - x) ) yields ( du = (2x - x^2) , dx ).
- ( dv = \cos(n\pi x) , dx ) integrates to ( v = \frac{1}{n\pi} \sin(n\pi x) ).
- Tabular Integration Process
Using the tabular integration method, we arrange:
| ( u ) | ( dv ) |
|---|---|
| ( x^2(1-x) ) | ( \frac{1}{n\pi} \sin(n\pi x) ) |
| ( 2x - x^2 ) | ( -\frac{1}{(n\pi)^2} \cos(n\pi x) ) |
| ( 2 - 2x ) | ( -\frac{1}{(n\pi)^3} \sin(n\pi x) ) |
Then, compute the integral using the alternating signs of this arrangement.
- Trigonometric Substitution for Integral
For the integral
$$ \int \sqrt{1 - x^2} , dx, $$
use the substitution ( x = \sin(\theta) ) so that ( dx = \cos(\theta) , d\theta ). Thus, the integral becomes:
$$ \int \sqrt{1 - \sin^2(\theta)} \cos(\theta) , d\theta = \int \cos^2(\theta) , d\theta. $$
- Solve the Integral
Use the identity ( \cos^2(\theta) = \frac{1}{2}(1 + \cos(2\theta)) ):
$$ \int \cos^2(\theta) , d\theta = \frac{1}{2}\left(\theta + \frac{1}{2} \sin(2\theta)\right) + C. $$
Substituting back ( \theta = \arcsin(x) ):
$$ \int \sqrt{1 - x^2} , dx = \frac{1}{2} \left(\arcsin(x) + \frac{x}{2} \sqrt{1 - x^2}\right) + C. $$
- Finding Minors of the Matrix
To find the minors of matrix ( A = \begin{bmatrix} 3 & 4 & -1 \ 1 & 0 & 3 \ 2 & 5 & -4 \end{bmatrix} ), compute the determinant of the ( 2 \times 2 ) submatrices obtained by removing one row and one column for each element.
- Minor for ( M_{11} ): Determinant of ( \begin{bmatrix} 0 & 3 \ 5 & -4 \end{bmatrix} = (0)(-4) - (3)(5) = -15 ).
- Minor for ( M_{12} ): Determinant of ( \begin{bmatrix} 1 & 3 \ 2 & -4 \end{bmatrix} = (1)(-4) - (3)(2) = -10 ).
- Minor for ( M_{13} ): Determinant of ( \begin{bmatrix} 1 & 0 \ 2 & 5 \end{bmatrix} = (1)(5) - (0)(2) = 5 ).
Calculate and repeat for rows 2 and 3 to find all minors.
-
(a_n) evaluates to a combination of sine and cosine terms from tabular integration.
-
The integral evaluates to:
$$ \int \sqrt{1 - x^2} , dx = \frac{1}{2} \left(\arcsin(x) + \frac{x}{2} \sqrt{1 - x^2}\right) + C. $$
- The minors of matrix ( A ) are:
- ( M_{11} = -15 )
- ( M_{12} = -10 )
- ( M_{13} = 5 ) (Continue similarly for other minors)
More Information
The tabular integration technique is helpful for integrating products of polynomial and trigonometric functions. The trigonometric substitution is a powerful technique for integrating functions involving square roots, particularly ( \sqrt{1 - x^2} ). The calculation of minors is essential in determinant and matrix theory, which is widely used in linear algebra.
Tips
- Failing to correctly apply the signs in tabular integration. Make sure to alternate signs properly.
- Not substituting back to original variables after integrating in trigonometric substitution. Always revert to the original variable.
- Forgetting to calculate all minors for the matrix. Ensure each minor is computed for every element by removing the associated row and column.
AI-generated content may contain errors. Please verify critical information