1. Evaluate the limit: lim (x->0) [x * tan^2(5x^2) / sin^5(2x)] 2. Evaluate the limit: lim (x->-inf) [x * 3^x / (3^x + 9^x)]
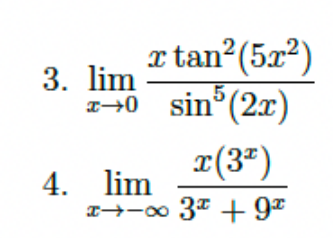
Understand the Problem
The image contains two limit problems that require evaluation. Specifically, the first problem involves trigonometric functions and the second involves exponential functions. Both will likely require algebraic manipulation and the application of standard limit techniques such as L'Hôpital's Rule or special trigonometric limits.
Answer
3. $\frac{25}{32}$ 4. $-\infty$
Answer for screen readers
- $\frac{25}{32}$
- $-\infty$
Steps to Solve
Here's how to solve the two limit problems step-by-step:
Problem 3: $\lim_{x\to 0} \frac{x \tan^2(5x^2)}{\sin^5(2x)}$
- Rewrite the limit using known limit properties
We can rewrite the limit as follows: $$ \lim_{x\to 0} \frac{x \tan^2(5x^2)}{\sin^5(2x)} = \lim_{x\to 0} x \cdot \frac{\tan^2(5x^2)}{\sin^5(2x)} $$
- Use the small angle approximations: $\tan(x) \approx x$ and $\sin(x) \approx x$ as $x\to 0$
As $x \to 0$, we have $\tan(5x^2) \approx 5x^2$ and $\sin(2x) \approx 2x$. Therefore: $$ \lim_{x\to 0} \frac{x \tan^2(5x^2)}{\sin^5(2x)} \approx \lim_{x\to 0} \frac{x (5x^2)^2}{(2x)^5} $$
- Simplify the expression
Simplify the expression inside the limit: $$ \lim_{x\to 0} \frac{x (25x^4)}{32x^5} = \lim_{x\to 0} \frac{25x^5}{32x^5} $$
- Cancel out the $x^5$ terms $$ \lim_{x\to 0} \frac{25}{32} = \frac{25}{32} $$
Problem 4: $\lim_{x\to -\infty} \frac{x(3^x)}{3^x + 9^x}$
- Rewrite $9^x$ as $(3^2)^x = (3^x)^2$
$$ \lim_{x\to -\infty} \frac{x(3^x)}{3^x + (3^x)^2} $$
- Factor out $3^x$ from the denominator
$$ \lim_{x\to -\infty} \frac{x(3^x)}{3^x(1 + 3^x)} $$
- Cancel out $3^x$ from the numerator and denominator
$$ \lim_{x\to -\infty} \frac{x}{1 + 3^x} $$
- Evaluate the limit as $x \to -\infty$
As $x \to -\infty$, $3^x \to 0$. Therefore: $$ \lim_{x\to -\infty} \frac{x}{1 + 3^x} = \frac{-\infty}{1 + 0} = -\infty $$
- $\frac{25}{32}$
- $-\infty$
More Information
The first limit evaluates to a finite value, indicating the rates at which the numerator and denominator approach zero are comparable. The second limit trends to negative infinity as $x$ becomes increasingly negative.
Tips
- For problem 3, a common mistake is incorrectly applying L'Hôpital's Rule repeatedly, which can lead to more complex expressions without simplification. The small angle approximations are much more efficient here.
- For problem 4, a common mistake is not recognizing that as $x \to -\infty$, $3^x \to 0$. Also, not correctly simplifying the exponential terms.
AI-generated content may contain errors. Please verify critical information