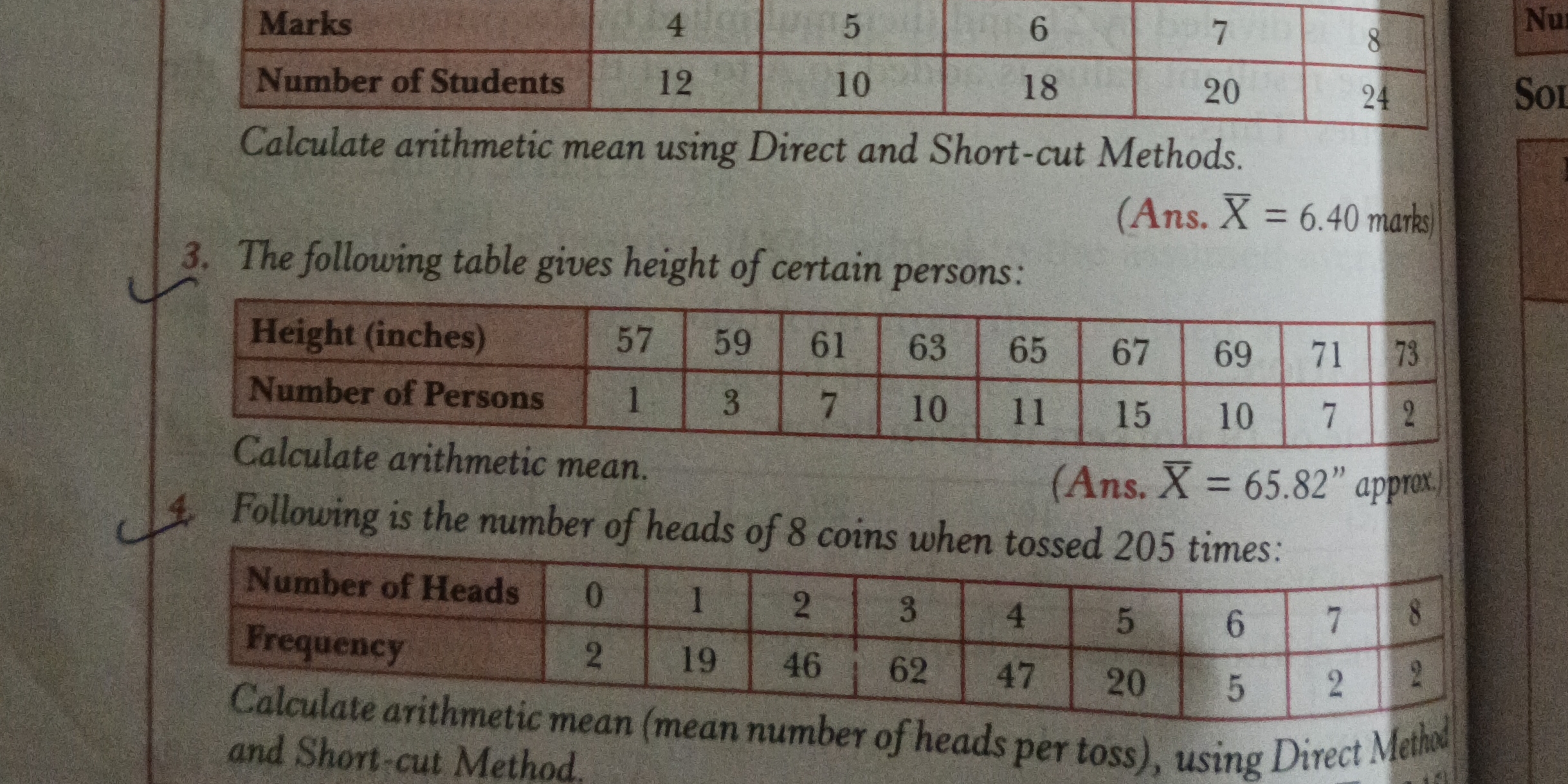
1. Calculate the arithmetic mean for the following data using direct and short-cut methods: Marks: 4, 5, 6, 7, 8 Number of Students: 12, 10, 18, 20, 24 2. Calculate the arithmeti... 1. Calculate the arithmetic mean for the following data using direct and short-cut methods: Marks: 4, 5, 6, 7, 8 Number of Students: 12, 10, 18, 20, 24 2. Calculate the arithmetic mean for the following data: Height (inches): 57, 59, 61, 63, 65, 67, 69, 71, 73 Number of Persons: 1, 3, 7, 10, 11, 15, 10, 7, 2 3. Calculate the arithmetic mean (mean number of heads per toss) for the following data using the direct and short-cut methods: Number of Heads: 0, 1, 2, 3, 4, 5, 6, 7, 8 Frequency: 2, 19, 46, 62, 47, 20, 5, 2, 2

Question image

Understand the Problem

The image presents two problems that involve calculating the arithmetic mean from given data. The first problem (labeled as 3) provides heights (in inches) and the number of persons for each height, asking for the arithmetic mean. The second problem (labeled as 4) gives the number of heads obtained when tossing 8 coins 205 times, along with the observed frequency of each outcome, and asks for the arithmetic mean using both the Direct and Short-cut methods.

Answer

Problem 1: $\text{Mean} \approx 6.40$ Problem 2: $\text{Mean} \approx 65.82$ Problem 3: $\text{Mean} \approx 3.146$
Answer for screen readers

Problem 1: $\text{Mean} \approx 6.40$ marks Problem 2: $\text{Mean} \approx 65.82$ inches Problem 3: $\text{Mean} \approx 3.146$ heads

Steps to Solve

Problem 1: (Marks and Students)

  1. Direct Method: Calculate the product of Marks and Number of Students Multiply each mark by the corresponding number of students.

$4 \times 12 = 48$ $5 \times 10 = 50$ $6 \times 18 = 108$ $7 \times 20 = 140$ $8 \times 24 = 192$

  1. Direct Method: Sum the products Add all the products calculated in the previous step.

$48 + 50 + 108 + 140 + 192 = 538$

  1. Direct Method: Sum the Number of Students Add the number of students.

$12 + 10 + 18 + 20 + 24 = 84$

  1. Direct Method: Calculate the mean Divide the sum of the products by the sum of the number of students.

$\text{Mean} = \frac{538}{84} \approx 6.40$

  1. Short-cut Method: Choose an assumed mean Let's choose $A = 6$ as the assumed mean.

  2. Short-cut Method: Calculate deviations from the assumed mean ($d_i = x_i - A$)

$d_1 = 4 - 6 = -2$ $d_2 = 5 - 6 = -1$ $d_3 = 6 - 6 = 0$ $d_4 = 7 - 6 = 1$ $d_5 = 8 - 6 = 2$

  1. Short-cut Method: Multiply deviations by the number of students

$(-2) \times 12 = -24$ $(-1) \times 10 = -10$ $0 \times 18 = 0$ $1 \times 20 = 20$ $2 \times 24 = 48$

  1. Short-cut Method: Sum the products of deviations and frequencies $-24 - 10 + 0 + 20 + 48 = 34$

  2. Short-cut Method: Apply the formula

$\text{Mean} = A + \frac{\sum f_i d_i}{\sum f_i}$ $\text{Mean} = 6 + \frac{34}{84} = 6 + 0.4047 \approx 6.40$

Problem 2: (Heights and Persons)

  1. Calculate the product of Height and Number of Persons Multiply each height by the corresponding number of persons.

$57 \times 1 = 57$ $59 \times 3 = 177$ $61 \times 7 = 427$ $63 \times 10 = 630$ $65 \times 11 = 715$ $67 \times 15 = 1005$ $69 \times 10 = 690$ $71 \times 7 = 497$ $73 \times 2 = 146$

  1. Sum the products Add all the products calculated in the previous step.

$57 + 177 + 427 + 630 + 715 + 1005 + 690 + 497 + 146 = 4344$

  1. Sum the Number of Persons Add the number of persons.

$1 + 3 + 7 + 10 + 11 + 15 + 10 + 7 + 2 = 66$

  1. Calculate the mean Divide the sum of the products by the sum of the number of persons.

$\text{Mean} = \frac{4344}{66} \approx 65.82$

Problem 3: (Number of Heads and Frequency)

  1. Direct Method: Calculate the product of Number of Heads and Frequency Multiply each number of heads by the corresponding frequency.

$0 \times 2 = 0$ $1 \times 19 = 19$ $2 \times 46 = 92$ $3 \times 62 = 186$ $4 \times 47 = 188$ $5 \times 20 = 100$ $6 \times 5 = 30$ $7 \times 2 = 14$ $8 \times 2 = 16$

  1. Direct Method: Sum the products Add all the products calculated in the previous step.

$0 + 19 + 92 + 186 + 188 + 100 + 30 + 14 + 16 = 645$

  1. Direct Method: Sum the Frequencies Add the frequencies.

$2 + 19 + 46 + 62 + 47 + 20 + 5 + 2 + 2 = 205$

  1. Direct Method: Calculate the mean Divide the sum of the products by the sum of the frequencies.

$\text{Mean} = \frac{645}{205} \approx 3.146$

  1. Short-cut Method: Choose an assumed mean Let's choose $A = 3$ as the assumed mean.

  2. Short-cut Method: Calculate deviations from the assumed mean ($d_i = x_i - A$)

$d_1 = 0 - 3 = -3$ $d_2 = 1 - 3 = -2$ $d_3 = 2 - 3 = -1$ $d_4 = 3 - 3 = 0$ $d_5 = 4 - 3 = 1$ $d_6 = 5 - 3 = 2$ $d_7 = 6 - 3 = 3$ $d_8 = 7 - 3 = 4$ $d_9 = 8 - 3 = 5$

  1. Short-cut Method: Multiply deviations by the frequencies

$(-3) \times 2 = -6$ $(-2) \times 19 = -38$ $(-1) \times 46 = -46$ $0 \times 62 = 0$ $1 \times 47 = 47$ $2 \times 20 = 40$ $3 \times 5 = 15$ $4 \times 2 = 8$ $5 \times 2 = 10$

  1. Short-cut Method: Sum the products of deviations and frequencies $-6 - 38 - 46 + 0 + 47 + 40 + 15 + 8 + 10 = 30$

  2. Short-cut Method: Apply the formula

$\text{Mean} = A + \frac{\sum f_i d_i}{\sum f_i}$ $\text{Mean} = 3 + \frac{30}{205} = 3 + 0.1463 \approx 3.146$

Problem 1: $\text{Mean} \approx 6.40$ marks Problem 2: $\text{Mean} \approx 65.82$ inches Problem 3: $\text{Mean} \approx 3.146$ heads

More Information

The arithmetic mean is a measure of central tendency, providing a 'typical' value that summarizes a dataset. Both the direct and short-cut methods will provide the same mean. The short-cut method simplifies calculations, especially with large numbers, by using an assumed mean.

Tips

  • Forgetting to multiply the values by their corresponding frequencies.
  • Incorrectly summing the products or frequencies.
  • Making errors in arithmetic calculations, especially when using the short-cut method with negative deviations.
  • Choosing a complicated assumed mean for the short-cut method, which defeats the purpose of simplifying calculations.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!
Use Quizgecko on...
Browser
Open
Browser
Browser