∫(1 + 3x)x² dx
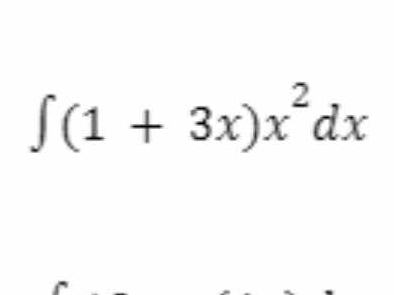
Understand the Problem
The question is asking us to evaluate the integral of the function (1 + 3x)x² with respect to x. This involves finding the antiderivative of the given expression.
Answer
The integral evaluates to $$\frac{x^3}{3} + \frac{3x^4}{4} + C$$.
Answer for screen readers
The final answer to the integral is: $$\frac{x^3}{3} + \frac{3x^4}{4} + C$$
Steps to Solve
- Distribute the terms
We start by distributing $(1 + 3x)$ with $x^2$. This gives us: $$(1 + 3x)x^2 = x^2 + 3x^3$$
- Rewrite the integral
Now we can rewrite the integral using the distributed form: $$\int (1 + 3x)x^2 , dx = \int (x^2 + 3x^3) , dx$$
- Integrate each term separately
Next, we integrate each term in the expression:
-
The integral of $x^2$ is: $$\int x^2 , dx = \frac{x^3}{3}$$
-
The integral of $3x^3$ is: $$\int 3x^3 , dx = 3 \cdot \frac{x^4}{4} = \frac{3x^4}{4}$$
- Combine the results
Now we combine the results of the integrals: $$\int (1 + 3x)x^2 , dx = \frac{x^3}{3} + \frac{3x^4}{4} + C$$ where $C$ is the constant of integration.
The final answer to the integral is: $$\frac{x^3}{3} + \frac{3x^4}{4} + C$$
More Information
This integral represents the area under the curve of the function $(1 + 3x)x^2$ with respect to $x$. Finding antiderivatives is a fundamental concept in calculus, related to the concept of finding areas and solving differential equations.
Tips
- Forgetting to distribute: Many students may forget to distribute the terms correctly before integrating. Always ensure each term is accounted for after the distribution.
- Incorrect integration: Make sure to apply the power rule correctly. Remember that for any term $x^n$, the integral is $\frac{x^{n+1}}{n+1}$.
