∫(1 + 3x)x^2 dx
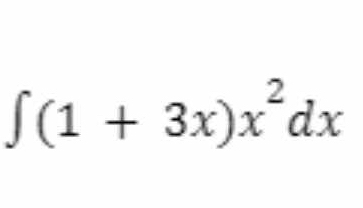
Understand the Problem
The question is asking to solve the integral of the expression (1 + 3x)x^2 with respect to x. This involves applying integration techniques to find the antiderivative of the given polynomial expression.
Answer
The integral evaluates to $$ \frac{x^{3}}{3} + \frac{3x^{4}}{4} + C $$
Answer for screen readers
The final result of the integral is:
$$ \frac{x^{3}}{3} + \frac{3x^{4}}{4} + C $$
Steps to Solve
- Expand the Expression
First, distribute (x^2) across the terms in the parentheses.
$$ (1 + 3x)x^2 = x^2 + 3x^3 $$
- Set Up the Integral
The integral can now be rewritten as:
$$ \int (x^2 + 3x^3) , dx $$
- Integrate Each Term
Apply the power rule of integration, which states that:
$$ \int x^n , dx = \frac{x^{n+1}}{n + 1} + C $$
Here, integrate each term:
- For (x^2):
$$ \int x^2 , dx = \frac{x^{3}}{3} $$
- For (3x^3):
$$ \int 3x^3 , dx = 3 \cdot \frac{x^{4}}{4} = \frac{3x^{4}}{4} $$
- Combine the Results
Now combine the results of the integrals:
$$ \int (x^2 + 3x^3) , dx = \frac{x^{3}}{3} + \frac{3x^{4}}{4} + C $$
The final result of the integral is:
$$ \frac{x^{3}}{3} + \frac{3x^{4}}{4} + C $$
More Information
This integral demonstrates the application of power rule for integration, which is essential for finding antiderivatives of polynomial functions. The constant (C) represents the arbitrary constant of integration, reflecting the family of all antiderivatives.
Tips
- Not expanding the expression first: It's common to forget to distribute (x^2) before integrating, leading to incorrect results.
- Incorrect application of the power rule: Make sure to increase the exponent by one and divide by the new exponent during integration.
