1 3/8 + 2 1/8
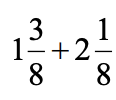
Understand the Problem
The question involves adding two fractions: 1 3/8 and 2 1/8. We will convert the mixed numbers to improper fractions, then find a common denominator and sum them.
Answer
The result of \( 1 \frac{3}{8} + 2 \frac{1}{8} \) is \( 3 \frac{1}{2} \).
Answer for screen readers
The final answer is ( 3 \frac{1}{2} ).
Steps to Solve
- Convert mixed numbers to improper fractions
To convert the mixed numbers ( 1 \frac{3}{8} ) and ( 2 \frac{1}{8} ) to improper fractions:
-
For ( 1 \frac{3}{8} ): $$ 1 \frac{3}{8} = \frac{1 \times 8 + 3}{8} = \frac{11}{8} $$
-
For ( 2 \frac{1}{8} ): $$ 2 \frac{1}{8} = \frac{2 \times 8 + 1}{8} = \frac{17}{8} $$
- Add the improper fractions
Now that we have the improper fractions, we can add them together:
$$ \frac{11}{8} + \frac{17}{8} = \frac{11 + 17}{8} = \frac{28}{8} $$
- Simplify the result
Now, we simplify ( \frac{28}{8} ):
$$ \frac{28 \div 4}{8 \div 4} = \frac{7}{2} $$
- Convert back to a mixed number (if necessary)
Finally, we convert ( \frac{7}{2} ) back to a mixed number:
$$ \frac{7}{2} = 3 \frac{1}{2} $$
The final answer is ( 3 \frac{1}{2} ).
More Information
Adding fractions can often require converting mixed numbers to improper fractions first. The process of simplifying fractions is important for obtaining the simplest form, which is useful in many mathematical applications.
Tips
- Failing to convert mixed numbers correctly into improper fractions.
- Forgetting to add the numerators correctly when the denominators are the same.
- Not simplifying the final fraction.
