1 - 1/3 + 1/3^2 - 1/3^3 + ... = ?
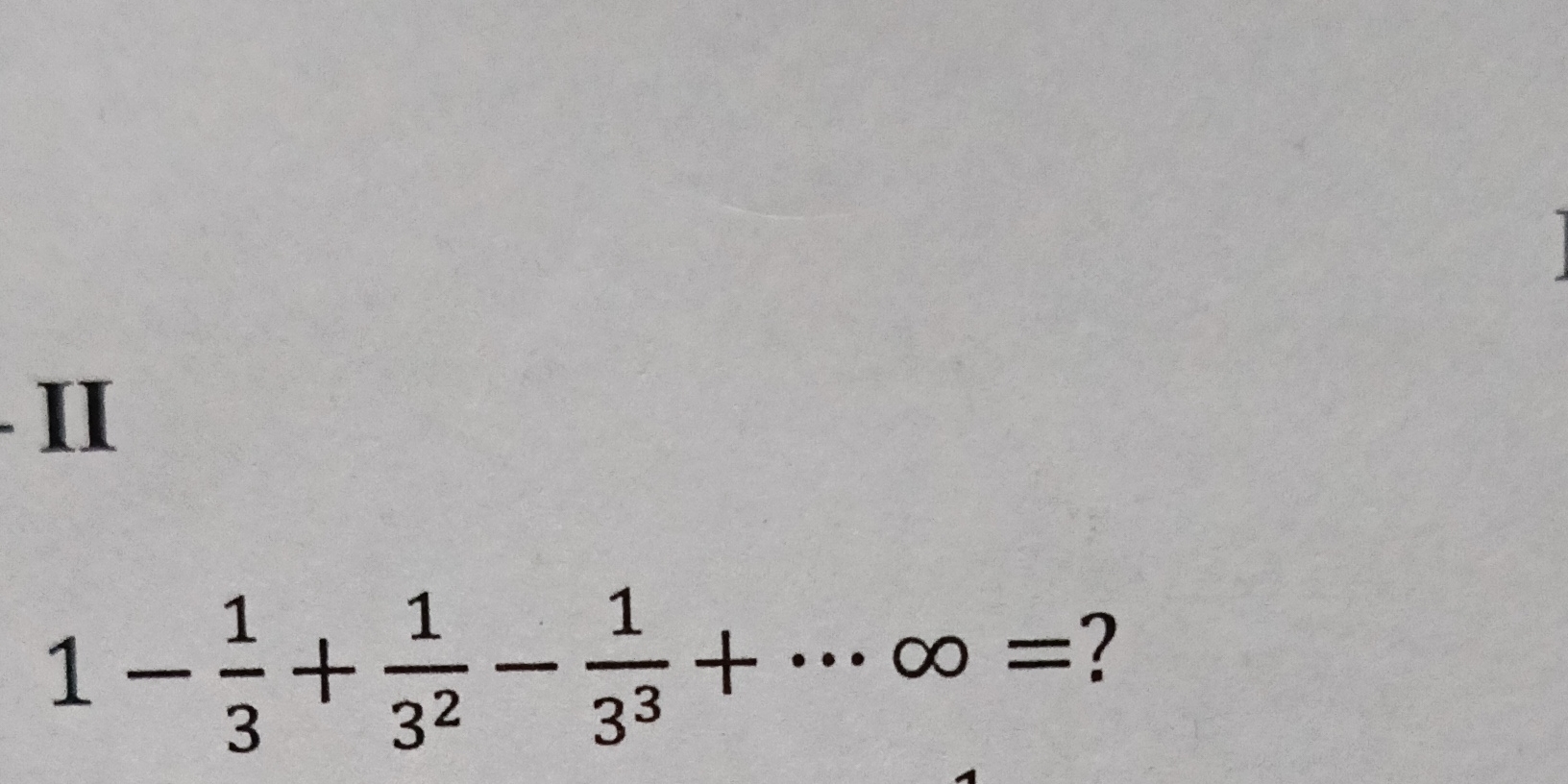
Understand the Problem
The question involves evaluating an infinite series that alternates between subtraction and addition, involving powers of fractions. We need to determine the sum of the series provided.
Answer
The sum of the series is $S = \frac{3}{4}$.
Answer for screen readers
The sum of the series is $S = \frac{3}{4}$.
Steps to Solve
- Identify the Pattern of the Series
The series can be expressed as:
$$ S = 1 - \frac{1}{3} + \frac{1}{3^2} - \frac{1}{3^3} + \cdots $$
This is an alternating series.
- Express the Series as a Geometric Series
Rewrite the series:
$$ S = 1 + \sum_{n=1}^{\infty} \left(-\frac{1}{3}\right)^n $$
Recognize that it is a geometric series with the first term $a = 1$ and a common ratio $r = -\frac{1}{3}$.
- Use the Formula for the Sum of an Infinite Geometric Series
The sum of an infinite geometric series can be calculated using the formula:
$$ S = \frac{a}{1 - r} $$
Plugging in the values for $a$ and $r$:
$$ S = \frac{1}{1 - \left(-\frac{1}{3}\right)} $$
- Calculate the Denominator
Simplify the denominator:
$$ 1 - \left(-\frac{1}{3}\right) = 1 + \frac{1}{3} = \frac{3}{3} + \frac{1}{3} = \frac{4}{3} $$
- Calculate the Sum
Now compute:
$$ S = \frac{1}{\frac{4}{3}} = \frac{3}{4} $$
The sum of the series is $S = \frac{3}{4}$.
More Information
This series demonstrates how alternating signs influence the sum of a geometric series. Infinite series are a fundamental concept in calculus and play a critical role in various mathematical applications.
Tips
- Misidentifying the type of series: Make sure to recognize alternating series versus standard geometric series.
- Incorrectly applying the geometric series sum formula: Ensure that the conditions for convergence are met (specifically, that the absolute value of the common ratio $|r| < 1$).
AI-generated content may contain errors. Please verify critical information