1 - 1/3 + 1/3^2 - 1/3^3 + ... ∞ = ?
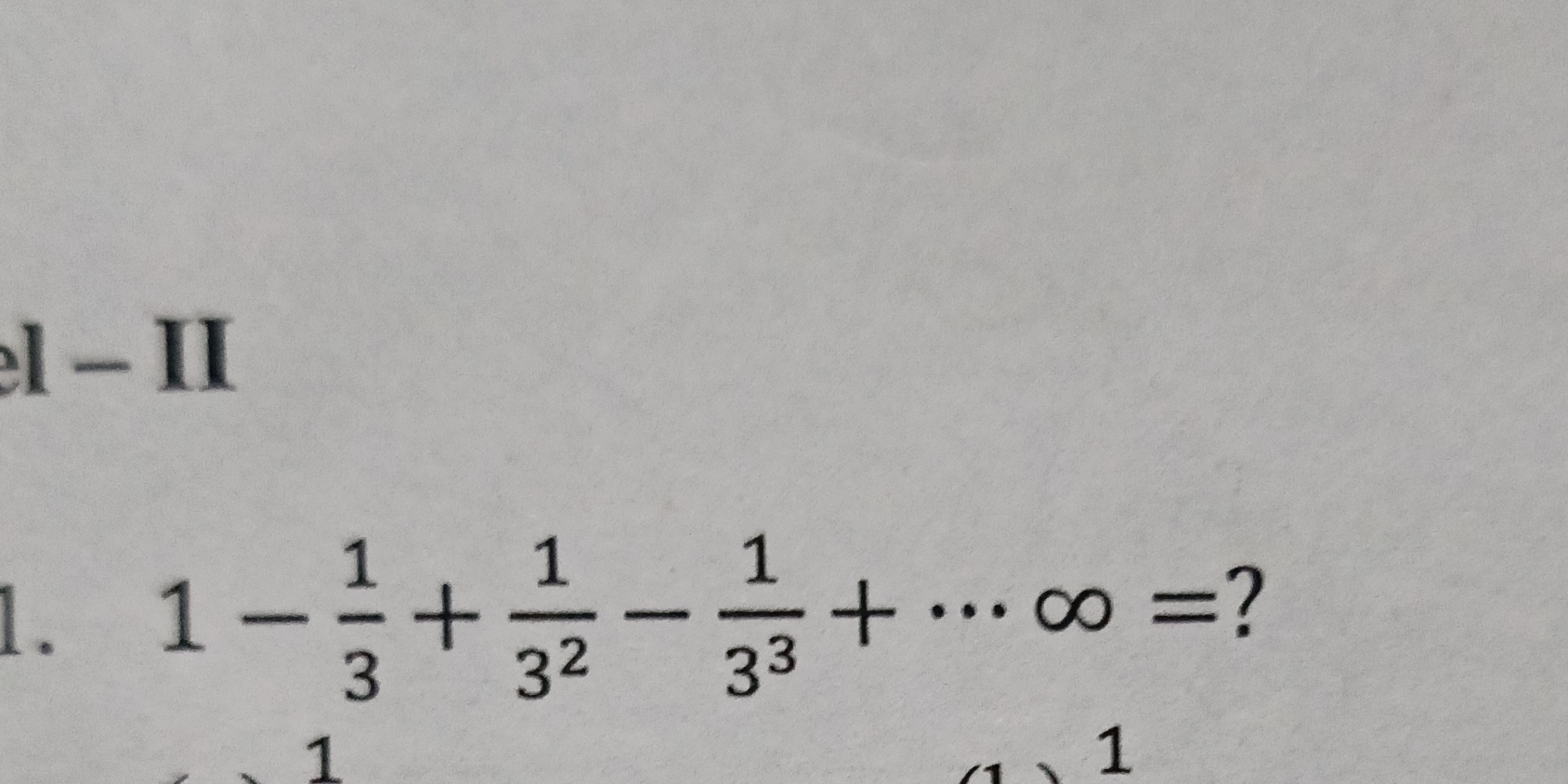
Understand the Problem
The question is asking for the sum of an infinite series that involves alternating fractions of decreasing powers of 3. This can be approached by recognizing the pattern in the series and applying concepts related to converging series.
Answer
The sum of the series is $S = \frac{3}{4}$.
Answer for screen readers
The sum of the infinite series is
$$ S = \frac{3}{4} $$
Steps to Solve
- Identify the Pattern of the Series
The series given is:
$$ S = 1 - \frac{1}{3} + \frac{1}{3^2} - \frac{1}{3^3} + \cdots $$
This can be rewritten as:
$$ S = 1 + \sum_{n=1}^\infty \left( -\frac{1}{3} \right)^n $$
- Recognize the Infinite Geometric Series
The series can be recognized as a geometric series of the form:
$$ a + ar + ar^2 + ar^3 + \ldots $$
where:
- ( a = 1 ) (the first term)
- ( r = -\frac{1}{3} ) (the common ratio)
- Apply the Formula for the Sum of a Geometric Series
The sum ( S ) of an infinite geometric series can be calculated using the formula:
$$ S = \frac{a}{1 - r} $$
where ( |r| < 1 ).
- Substituting Values into the Formula
Substituting ( a = 1 ) and ( r = -\frac{1}{3} ):
$$ S = \frac{1}{1 - \left(-\frac{1}{3}\right)} = \frac{1}{1 + \frac{1}{3}} = \frac{1}{\frac{4}{3}} = \frac{3}{4} $$
The sum of the infinite series is
$$ S = \frac{3}{4} $$
More Information
This series is an example of an alternating geometric series. It converges because the common ratio satisfies ( |r| < 1 ), which ensures that the series will approach a finite limit.
Tips
- Misunderstanding the Common Ratio: A common mistake is incorrectly identifying the common ratio. Make sure to check the sign and magnitude of terms.
- Forgetting the Convergence Condition: Not recognizing when a series converges can lead to incorrect conclusions about the sum.
AI-generated content may contain errors. Please verify critical information