1 - 1/3 + 1/3^2 - 1/3^3 + ... ∞ = ?
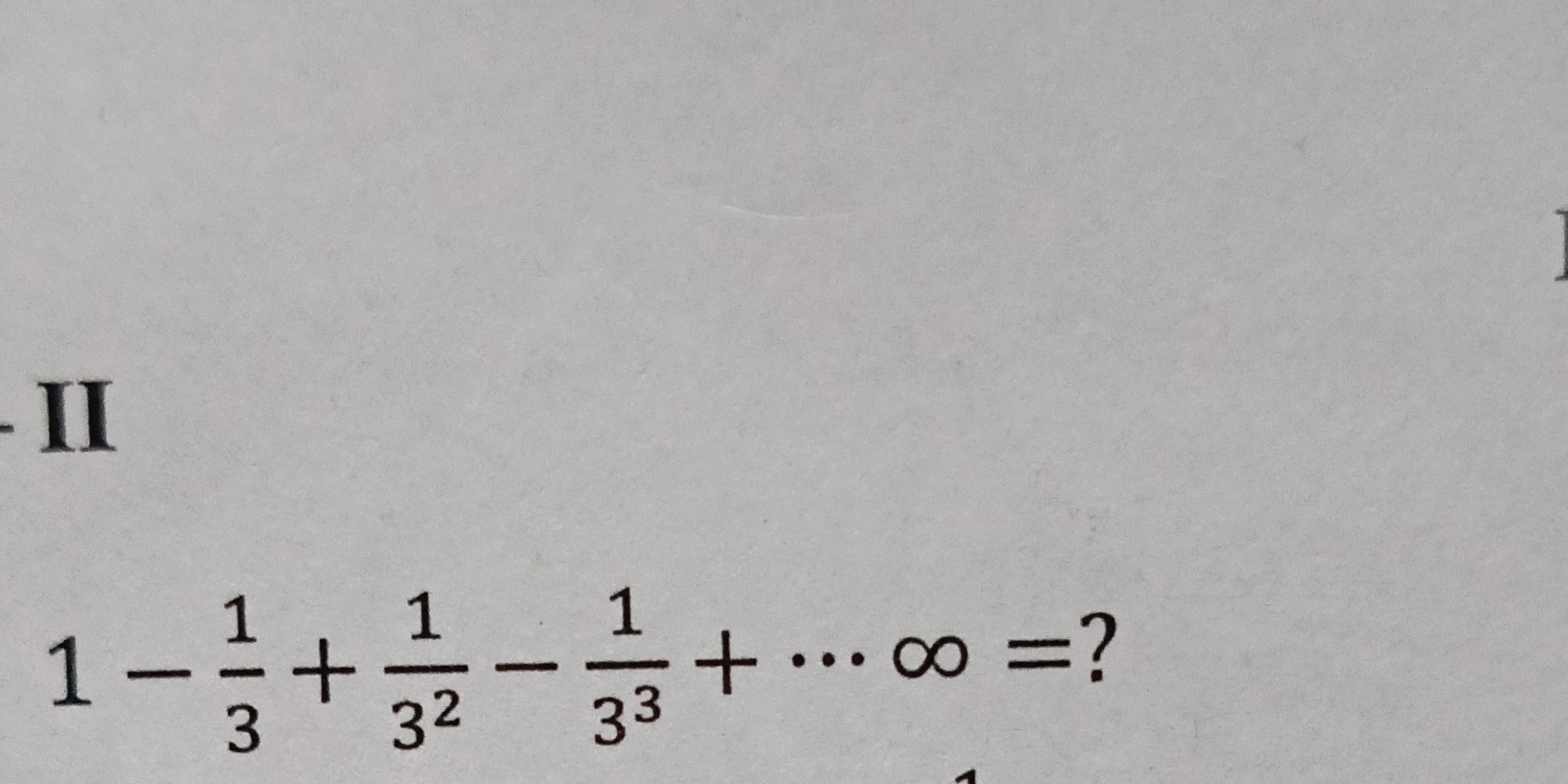
Understand the Problem
The question is asking us to solve an infinite series that starts with 1 and then involves a series of fractions decreasing by powers of 3. It appears to be a problem related to series or sequences in mathematics.
Answer
The sum of the series is $S = \frac{3}{4}$.
Answer for screen readers
The sum of the infinite series is $S = \frac{3}{4}$.
Steps to Solve
-
Write the Infinite Series The series can be expressed as: $$ S = 1 - \frac{1}{3} + \frac{1}{3^2} - \frac{1}{3^3} + \cdots $$
-
Recognize the Pattern This series is an infinite geometric series where the first term $a = 1$ and the common ratio $r = -\frac{1}{3}$.
-
Use the Formula for the Sum of an Infinite Geometric Series The sum of an infinite geometric series can be calculated using the formula: $$ S = \frac{a}{1 - r} $$ where $|r| < 1$.
-
Substitute the Values Substituting the values into the formula: $$ S = \frac{1}{1 - \left(-\frac{1}{3}\right)} $$ This simplifies to: $$ S = \frac{1}{1 + \frac{1}{3}} = \frac{1}{\frac{4}{3}} = \frac{3}{4} $$
-
Final Calculation Thus, the sum of the infinite series is: $$ S = \frac{3}{4} $$
The sum of the infinite series is $S = \frac{3}{4}$.
More Information
This series demonstrates the properties of geometric series, where alternating signs occur due to the negative common ratio. The formula for the sum of an infinite geometric series only applies when the absolute value of the common ratio is less than one, ensuring convergence.
Tips
- Ignoring the Sign: Not accounting for the negative sign in the common ratio, leading to incorrect series terms.
- Misapplication of the Sum Formula: Using the formula without verifying that $|r| < 1$ can lead to incorrect assumptions about convergence.
AI-generated content may contain errors. Please verify critical information