1 - 1/3 + 1/3 - 1/3.
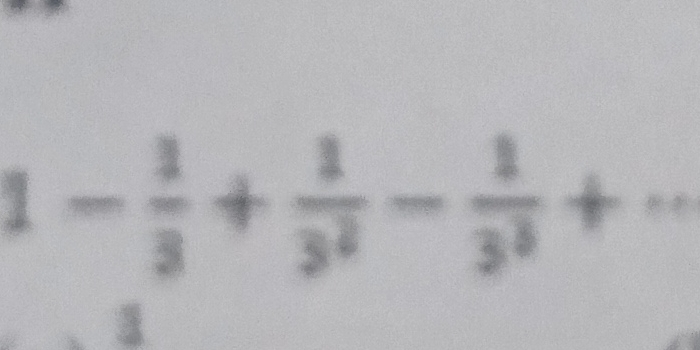
Understand the Problem
The question involves adding and subtracting fractions. The focus is on calculating the expression that includes fractions with a common denominator.
Answer
The final result is \( \frac{2}{3} \).
Answer for screen readers
The final answer is:
$$ \frac{2}{3} $$
Steps to Solve
- Write the expression clearly
The expression to solve is:
$$ 1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{3} $$
- Calculate the first operation
Start with the first part:
$$ 1 - \frac{1}{3} $$
Convert (1) to a fraction:
$$ 1 = \frac{3}{3} $$
Now perform the subtraction:
$$ \frac{3}{3} - \frac{1}{3} = \frac{2}{3} $$
- Add the next fraction
Now add ( \frac{1}{3} ) to ( \frac{2}{3} ):
$$ \frac{2}{3} + \frac{1}{3} = \frac{3}{3} $$
This simplifies to:
$$ \frac{3}{3} = 1 $$
- Subtract the final fraction
Now subtract ( \frac{1}{3} ):
$$ 1 - \frac{1}{3} $$
Convert (1) again:
$$ 1 = \frac{3}{3} $$
Perform the subtraction:
$$ \frac{3}{3} - \frac{1}{3} = \frac{2}{3} $$
The final answer is:
$$ \frac{2}{3} $$
More Information
The process involved converting whole numbers to fractions for easy computation and ensuring that all fractions had a common denominator for addition and subtraction.
Tips
- Forgetting to convert whole numbers into fractions.
- Miscalculating the addition or subtraction of fractions by neglecting the common denominator.
AI-generated content may contain errors. Please verify critical information