(1 1) • (x1) = (3) (2 2) (x2) (6)

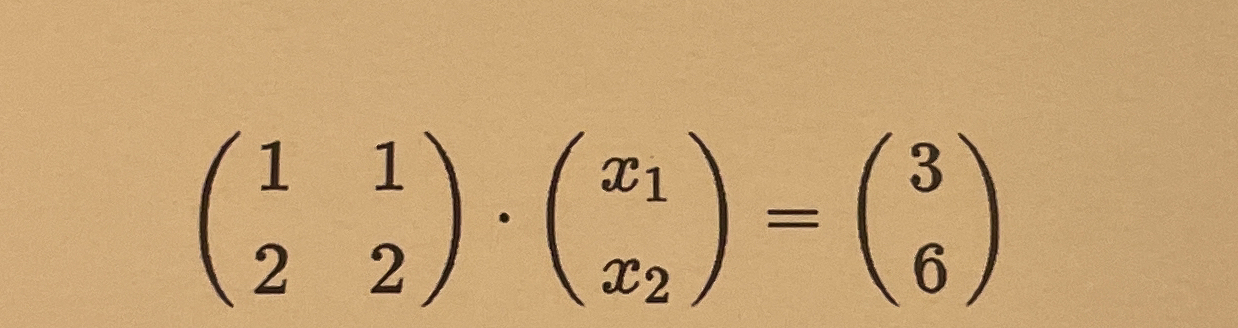
Understand the Problem

The question is asking to solve a system of linear equations represented by a matrix equation. The left side involves a multiplication of a 2x2 matrix with a 2x1 vector, and the result should equal the given 2x1 vector on the right. We need to find the values of x1 and x2 that satisfy this equation.

Answer

The solution to the system is given by $x_1 = t$ and $x_2 = 3 - t$ for any real number $t$.

Steps to Solve

Write the equations from the matrix product

From the given matrices, we have two equations. The first row gives us: $$ 1 \cdot x_1 + 1 \cdot x_2 = 3 $$

The second row gives us: $$ 2 \cdot x_1 + 2 \cdot x_2 = 6 $$

Simplify the equations

The second equation can be simplified by dividing everything by 2: $$ x_1 + x_2 = 3 $$

Now we have two identical equations:

$x_1 + x_2 = 3$
$x_1 + x_2 = 3$
Identify variables

From the equation $x_1 + x_2 = 3$, we can express $x_2$ in terms of $x_1$: $$ x_2 = 3 - x_1 $$

Choose a value for (x_1)

Since this is a system with infinite solutions, we can choose a value for $x_1$. Let's choose $x_1 = 0$: $$ x_2 = 3 - 0 = 3 $$

General solution

Alternatively, we express the solution as: $$ x_1 = t \quad \text{and} \quad x_2 = 3 - t $$ where (t) can be any real number.

The system of equations has infinitely many solutions expressed as: $$ x_1 = t, \quad x_2 = 3 - t $$ for any real number (t).

More Information

This system of equations is dependent, meaning that it doesn't have a unique solution. Instead, any value of (t) gives a corresponding value for (x_2) that satisfies both equations.

Tips

Ignoring infinite solutions: Since both equations are the same, a common mistake is assuming that there is a unique solution when there are actually infinitely many.
Confusing the relationships between variables: Another mistake is not correctly isolating one variable with respect to the other.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!