Understand the Problem
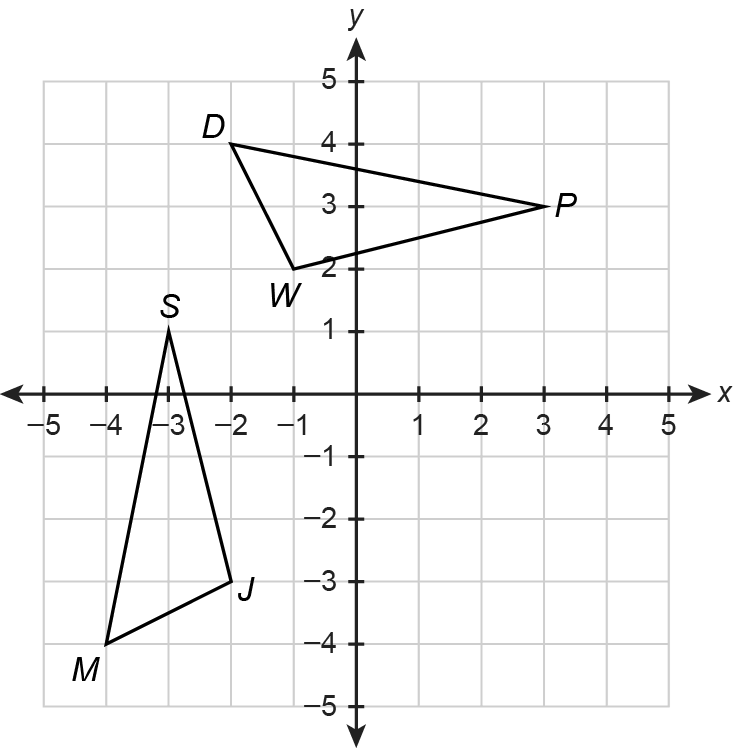
The image presents a coordinate plane with two geometric shapes marked with vertices labeled by letters. The question likely pertains to properties of these shapes or their relations in the coordinate system, possibly involving calculations like area or perimeter.
Answer
The areas of both triangles DWP and SMJ are equal and are $2$.
Answer for screen readers
The areas of both triangles DWP and SMJ are equal, with a value of $2$.
Steps to Solve
-
Identify the vertices' coordinates
- For triangle DWP, the vertices are:
- $D(1, 4)$
- $W(1, 2)$
- $P(3, 3)$
- For triangle SMJ, the vertices are:
- $S(-2, -3)$
- $M(-4, -5)$
- $J(-1, -4)$
- For triangle DWP, the vertices are:
-
Calculate the area of triangle DWP
- Use the formula for the area of a triangle given its vertices: $$ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| $$
- Plugging in the coordinates: $$ \text{Area}_{DWP} = \frac{1}{2} \left| 1(2 - 3) + 1(3 - 4) + 3(4 - 2) \right| $$
- Calculating: $$ = \frac{1}{2} \left| 1(-1) + 1(-1) + 3(2) \right| $$ $$ = \frac{1}{2} \left| -1 -1 + 6 \right| $$ $$ = \frac{1}{2} \left| 4 \right| = 2 $$
-
Calculate the area of triangle SMJ
- Using the same formula: $$ \text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| $$
- Plugging in the coordinates: $$ \text{Area}_{SMJ} = \frac{1}{2} \left| -2(-5 - -4) + -4(-4 - -3) + -1(-3 - -5) \right| $$
- Calculating: $$ = \frac{1}{2} \left| -2(-1) + -4(-1) + -1(2) \right| $$ $$ = \frac{1}{2} \left| 2 + 4 - 2 \right| $$ $$ = \frac{1}{2} \left| 4 \right| = 2 $$
-
Compare the areas
- Both triangles have equal area: $$ \text{Area}{DWP} = \text{Area}{SMJ} = 2 $$
The areas of both triangles DWP and SMJ are equal, with a value of $2$.
More Information
Both triangles have the same area despite their different shapes and positions on the coordinate plane. This illustrates the principle that the area is dependent on the vertices' positions rather than their layout.
Tips
- A common mistake is forgetting to use the absolute value in the area formula, which can lead to a negative area.
- Ensure that the coordinates are accurately input into the area formula to avoid calculation errors.
AI-generated content may contain errors. Please verify critical information