Understanding Venn Diagrams

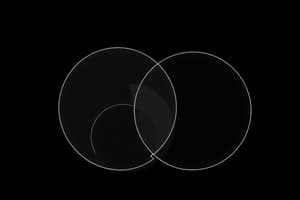
• Venn diagrams offer a visual representation of sets and their relationships using overlapping shapes, typically circles, inside a rectangle that symbolizes the universal set
• They aid in visually organizing data to simplify understanding relationships between different groups
• Overlapping circles in Venn diagrams illustrate the relationships between sets
• A rectangle represents the universal set, encompassing all elements under consideration
• Each circle corresponds to a set, while overlapping areas denote the intersection of sets
• The area outside the circles, yet within the rectangle, signifies elements outside any of the defined sets

Basic Set Operations

• Union (A ∪ B): Includes all elements in A, in B, or in both A and B
• Intersection (A ∩ B): Includes elements common to both A and B
• Complement (A'): Includes all elements in the universal set not in A
• Difference (A - B): Includes elements in A but not in B
• Symmetric Difference (A Δ B): Includes elements in either A or B, but not in both; can also be expressed as (A ∪ B) - (A ∩ B)

Problem-Solving with Venn Diagrams

• Used in solving problems related to set theory, logic, and data analysis
• Help visualize and simplifying complex relationships among data groups
• Identify sets, draw the Venn diagram with overlapping circles when solving problems
• Fill the Venn diagram, begin with the intersection of all sets
• Complete the remaining sections using provided data and set operations
• Use the diagram to answer questions, like finding the number of elements in a set or the intersection of sets

Applications of Venn Diagrams

• Used in mathematics for illustrating set theory concepts, probability, and statistics
• Used in logic for analyzing arguments, establishing validity, and depicting logical relationships
• Used in computer science for representing data structures, database queries, and algorithm design
• Used in business for market analysis, customer segmentation, and decision-making processes
• Used in education for teaching concepts, information organization, and improved comprehension

Steps for Solving Problems Using Venn Diagrams

• Read and Understand the Problem: Identify sets and relationships
• Draw the Venn Diagram: Include appropriate overlapping circles and labels
• Fill in the Intersections: Start with the intersection of all sets
• Use the Given Information: Perform necessary calculations for all sets
• Answer the Questions: Use the information to answer questions

Example Problem

• In a class of 30 students, 15 play football, 10 play basketball, and 5 play both football and basketball.
• Draw a Venn diagram to represent this scenario
• Find out how many students play neither sport

Solution

• Draw two overlapping circles labeled football (F) and basketball (B) inside a rectangle (U) for the universal set of 30 students
• The intersection of F and B is 5 (students playing both sports)
• For football circle F, the remainder is 15 - 5 = 10
• For basketball circle B, the remainder is 10 - 5 = 5
• Numbers in the circle added: 10 (football only) + 5 (both) + 5 (basketball only) = 20
• Subtract the total number for the unrepresented number of students: 30 - 20 = 10
• 10 students play neither football nor basketball

Benefits of Using Venn Diagrams

• Simplify complex problems via relationship visualization
• Logically organize information for understanding and remembering
• Solve problems in set theory, logic, and data analysis effectively
• Enhance communication and collaboration by visually representing data and relationships
• Improve decision-making with clear overviews of information

Common Mistakes to Avoid

• Misinterpreting problem statements and incorrectly identifying sets and relationships
• Filling in the Venn diagram incorrectly leading to inaccurate results
• Neglecting to double-check calculations and logic for errors
• Overlooking the universal set and external elements
• Overcomplicating the diagram affecting interpretation

Advanced Venn Diagrams

• Use more complex diagrams when involving more than three sets
• Drawing these diagrams and filling them accurately can be challenging
• Use colors or shading when distinguishing regions in the diagram
• Create variations such as Euler diagrams, where not all intersections are represented

Tips for Creating Effective Venn Diagrams

• Use clear labels making it easy to understand the meaning of each circle/set
• Select circle sizes to reflect relative sizes of sets
• Correctly use overlapping circles to represent set intersections
• Use varying colors to distinguish regions of the diagram
• Keep the diagram simple and easy to understand, avoiding unnecessary details