Teoría de Conjuntos: Fundamentos

Capítulo 1: Teoría de Conjuntos

• Un conjunto es una colección de objetos llamados elementos.

Notación

• $x \in A$: x es un elemento de A.
• $x \notin A$: x no es un elemento de A.
• $A = B$: A y B tienen los mismos elementos.
• $A \subseteq B$: A es un subconjunto de B, lo que significa que todo elemento de A también está en B.
• $A \subset B$: A es un subconjunto propio de B, donde A está contenido en B, pero A no es igual a B.
• $\emptyset$: Representa el conjunto vacío, que no contiene elementos.

Operaciones Entre Conjuntos

• Estas operaciones se aplican a subconjuntos A y B de un conjunto universal U.
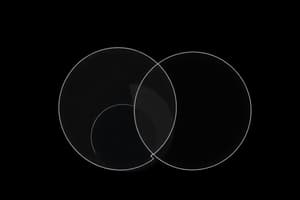
• Unión: $A \cup B = {x \in U \mid x \in A \text{ o } x \in B}$, que contiene todos los elementos en A o B.
• Intersección: $A \cap B = {x \in U \mid x \in A \text{ y } x \in B}$, contiene los elementos comunes a A y B.
• Diferencia: $A \setminus B = {x \in U \mid x \in A \text{ y } x \notin B}$, contiene los elementos en A que no están en B.
• Complemento: $A^c = {x \in U \mid x \notin A}$, que incluye los elementos en U que no están en A.

Leyes de De Morgan

• $(A \cup B)^c = A^c \cap B^c$
• $(A \cap B)^c = A^c \cup B^c$

Conjuntos Disjuntos

• Dos conjuntos A y B son disjuntos si su intersección es el conjunto vacío ($A \cap B = \emptyset$).

Partición de un Conjunto

• Una partición de un conjunto A es una colección de subconjuntos disjuntos ${A_i}{i \in I}$ de A tal que $A = \bigcup{i \in I} A_i$.

1.2. Producto Cartesiano

• Es el conjunto de todos los pares ordenados $(a, b)$ donde $a \in A$ y $b \in B$.
• Notación: $A \times B = {(a, b) \mid a \in A, b \in B}$
• Ejemplo: Si $A = {1, 2}$ y $B = {a, b, c}$, entonces $A \times B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)}$.
• El producto cartesiano de $n$ conjuntos $A_1, A_2, \dots, A_n$ es el conjunto de todas las $n$-tuplas ordenadas $(a_1, a_2, \dots, a_n)$ donde $a_i \in A_i$ para cada $i = 1, 2, \dots, n$.
• Notación: $A_1 \times A_2 \times \dots \times A_n = {(a_1, a_2, \dots, a_n) \mid a_i \in A_i, i = 1, 2, \dots, n}$

1.3. Relaciones

• Una relación $R$ de un conjunto $A$ a un conjunto $B$ es un subconjunto del producto cartesiano $A \times B$.
• Si $(a, b) \in R$, se dice que $a$ está relacionado con $b$ y se escribe $a R b$.
• Ejemplo: Sea $A = {1, 2, 3}$ y $B = {a, b}$. Entonces $R = {(1, a), (2, b)}$ es una relación de $A$ a $B$. Aquí, $1Ra$ y $2Rb$.

Relaciones en un Conjunto

• Una relación definida en un conjunto A es un subconjunto de A x A.
• Ejemplo: En el conjunto $A = {1, 2, 3}$, la relación $R = {(1, 1), (1, 2), (2, 3)}$ ilustra una relación dentro de A.

Propiedades de las Relaciones

• Para una relación R en un conjunto A:
  • Reflexiva: (a, a) ∈ R para todo a ∈ A.
  • Simétrica: Si (a, b) ∈ R, entonces (b, a) ∈ R.
  • Antisimétrica: Si (a, b) ∈ R y (b, a) ∈ R, entonces a = b.
  • Transitiva: Si (a, b) ∈ R y (b, c) ∈ R, entonces (a, c) ∈ R.

Relaciones de Equivalencia

• Una relación R en un conjunto A es de equivalencia si cumple con ser reflexiva, simétrica y transitiva.
• Ejemplo: En el conjunto de los enteros $\mathbb{Z}$, la relación $a R b$ si $a \equiv b \pmod{n}$ define una relación de equivalencia, donde n es un entero positivo.

Clases de Equivalencia

• Para una relación de equivalencia R en un conjunto A, la clase de equivalencia de un elemento a ∈ A, denotada como [a], es el conjunto de todos los elementos de A relacionados con a: $[a] = {x \in A \mid x R a}$
• Teorema: Las clases de equivalencia de una relación de equivalencia R en un conjunto A forman una partición de A.

1.4. Funciones

• Una función $f$ de un conjunto A a un conjunto B es una relación de A a B tal que para cada $a \in A$ existe un único $b \in B$ tal que $(a, b) \in f$. Se escribe $f: A \to B$ y se denota $f(a) = b$.

Terminología

• $A$: Dominio de $f$
• $B$: Codominio de $f$
• ${f(a) \mid a \in A}$: Rango de $f$

Tipos de Funciones

• Inyectiva (uno a uno): Si $f(a_1) = f(a_2)$ implica que $a_1 = a_2$.
• Sobreyectiva (suprayectiva o exhaustiva): Si para todo $b \in B$ existe $a \in A$ tal que $f(a) = b$.
• Biyectiva: Si es inyectiva y sobreyectiva.

Composición de Funciones

• Dadas $f: A \to B$ y $g: B \to C$, la composición $g \circ f: A \to C$ se define como $(g \circ f)(a) = g(f(a))$ para todo $a \in A$.

Función Inversa

• Para una función biyectiva $f: A \to B$, la función inversa $f^{-1}: B \to A$ se define como $f^{-1}(b) = a$ si y sólo si $f(a) = b$.

1.5. Cardinalidad

• Dos conjuntos A y B tienen la misma cardinalidad si existe una función biyectiva $f: A \to B$. Se escribe $|A| = |B|$.
• Un conjunto A es finito si existe un entero no negativo $n$ tal que $|A| = |{1, 2, \dots, n}|$. En este caso, se dice que $A$ tiene cardinalidad $n$ y se escribe $|A| = n$.
• Un conjunto A es infinito si no es finito.
• Un conjunto A es numerable si existe una función biyectiva $f: \mathbb{N} \to A$, donde $\mathbb{N}$ es el conjunto de los números naturales. En este caso, se dice que $A$ tiene cardinalidad $\aleph_0$ (álef cero) y se escribe $|A| = \aleph_0$.
• Un conjunto $A$ es no numerable si no es finito ni numerable.
• Ejemplo: El conjunto de los números reales $\mathbb{R}$ es no numerable. Tiene cardinalidad $c$ (cardinalidad del continuo).
• Teorema: Si A y B son conjuntos numerables, entonces $A \times B$ es numerable.
• Teorema: El conjunto de los números racionales $\mathbb{Q}$ es numerable.