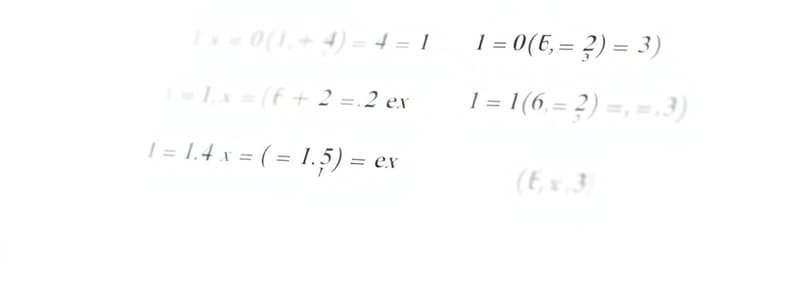Podcast
Questions and Answers
Solve for $x$: $3(x + 2) = 5x - 4$
Solve for $x$: $3(x + 2) = 5x - 4$
- $x = 8$
- $x = 5$ (correct)
- $x = 6$
- $x = 7$
The expansion of $(a + b)^2$ is $a^2 + b^2$
The expansion of $(a + b)^2$ is $a^2 + b^2$
False (B)
Expand and simplify: $(x + 3)(x - 4)$
Expand and simplify: $(x + 3)(x - 4)$
x^2 - x - 12
If $2x + 5 = 11$, then $x$ = ____
If $2x + 5 = 11$, then $x$ = ____
Match the following expressions with their simplified forms:
Match the following expressions with their simplified forms:
Solve for $x$: $3x + 7 = 22$
Solve for $x$: $3x + 7 = 22$
Expand the following expression: $4(2x - 3)$
Expand the following expression: $4(2x - 3)$
Solve for $x$: $5x - 10 = 2x + 5$. The value of x is ______.
Solve for $x$: $5x - 10 = 2x + 5$. The value of x is ______.
Match the expression with its expanded form:
Match the expression with its expanded form:
Expand: $2(3y - 5)$
Expand: $2(3y - 5)$
Solve for $x$: $5x - 9 = 3x + 5$. Therefore, x = ______
Solve for $x$: $5x - 9 = 3x + 5$. Therefore, x = ______
Match the equation to its solution set:
Match the equation to its solution set:
The expression $(a + b)^2$ is equivalent to $a^2 + b^2$.
The expression $(a + b)^2$ is equivalent to $a^2 + b^2$.
Expand and simplify: $2(x - 3) + 5(x + 2)$
Expand and simplify: $2(x - 3) + 5(x + 2)$
If $y = 4x - 9$ and $x = 3$, then $y$ = ____.
If $y = 4x - 9$ and $x = 3$, then $y$ = ____.
Match the following expressions with their expanded forms:
Match the following expressions with their expanded forms:
Solve for $x$: $5x - 10 = 3x + 4$, $x$ = ______
Solve for $x$: $5x - 10 = 3x + 4$, $x$ = ______
What is the solution to the linear equation $3x + 7 = 22$?
What is the solution to the linear equation $3x + 7 = 22$?
Is the expression $(a + b)^2$ equivalent to $a^2 + b^2$?
Is the expression $(a + b)^2$ equivalent to $a^2 + b^2$?
Solve for $y$: $2y - 5 = 11$. Therefore, $y$ = _______
Solve for $y$: $2y - 5 = 11$. Therefore, $y$ = _______
Which of the following is the expanded form of the binomial $(2x - 3)^2$?
Which of the following is the expanded form of the binomial $(2x - 3)^2$?
Expand the following expression: $4(2x + 3y - 5)$
Expand the following expression: $4(2x + 3y - 5)$
Is $3x + 5 = 2x - 1$ equivalent to $x = -6$?
Is $3x + 5 = 2x - 1$ equivalent to $x = -6$?
Solve for x: $2(x + 3) = 16$, $x$ = _____
Solve for x: $2(x + 3) = 16$, $x$ = _____
What is the solution to the equation $3x + 7 = 22$?
What is the solution to the equation $3x + 7 = 22$?
Is the following statement true or false? $(a + b)^2 = a^2 + b^2$
Is the following statement true or false? $(a + b)^2 = a^2 + b^2$
Solve for x: $5x - 10 = 2x + 5$. x = _______
Solve for x: $5x - 10 = 2x + 5$. x = _______
Flashcards
What is a linear equation?
What is a linear equation?
An equation where the highest power of the variable is 1. When graphed, it forms a straight line.
What is a binomial?
What is a binomial?
An algebraic expression with two terms, connected by a plus or minus sign.
What does 'expanding brackets' mean?
What does 'expanding brackets' mean?
The process of multiplying each term inside the brackets by the term outside the brackets.
What is meant by simplifying?
What is meant by simplifying?
Signup and view all the flashcards
What does 'solving an equation' mean?
What does 'solving an equation' mean?
Signup and view all the flashcards
What is a constant?
What is a constant?
Signup and view all the flashcards
What is a coefficient?
What is a coefficient?
Signup and view all the flashcards
What are like terms?
What are like terms?
Signup and view all the flashcards
What is a solution to an equation?
What is a solution to an equation?
Signup and view all the flashcards
What is a variable?
What is a variable?
Signup and view all the flashcards
What is a term?
What is a term?
Signup and view all the flashcards
What is a 'solution'?
What is a 'solution'?
Signup and view all the flashcards
What does 'simplify' mean?
What does 'simplify' mean?
Signup and view all the flashcards
Expanding Brackets
Expanding Brackets
Signup and view all the flashcards
Combining Like Terms
Combining Like Terms
Signup and view all the flashcards
Simplifying Expressions
Simplifying Expressions
Signup and view all the flashcards
Solving Equations
Solving Equations
Signup and view all the flashcards
What is the coefficient?
What is the coefficient?
Signup and view all the flashcards
What is a 'root' of an equation?
What is a 'root' of an equation?
Signup and view all the flashcards
What is an identity?
What is an identity?
Signup and view all the flashcards
What is 'expanding'?
What is 'expanding'?
Signup and view all the flashcards
What does 'evaluating' mean?
What does 'evaluating' mean?
Signup and view all the flashcards
What is the additive identity?
What is the additive identity?
Signup and view all the flashcards
What is an equation?
What is an equation?
Signup and view all the flashcards
What is the Distributive Property?
What is the Distributive Property?
Signup and view all the flashcards
What is an extraneous solution?
What is an extraneous solution?
Signup and view all the flashcards
What is meant by 'inverse operations'?
What is meant by 'inverse operations'?
Signup and view all the flashcards
What is an identity equation?
What is an identity equation?
Signup and view all the flashcards
How to Expand Brackets
How to Expand Brackets
Signup and view all the flashcards
Solving simple linear equations
Solving simple linear equations
Signup and view all the flashcards
Expanding single brackets
Expanding single brackets
Signup and view all the flashcards
Combining algebraic terms
Combining algebraic terms
Signup and view all the flashcards
Binomial Expansion
Binomial Expansion
Signup and view all the flashcards
Solve an equation with variables on both sides
Solve an equation with variables on both sides
Signup and view all the flashcards
Study Notes
- Solving Linear Equations
- The objective is to isolate the variable on one side.
- Inverse operations reverse the operations on the variable.
- Addition and subtraction are inverse operations.
- Multiplication and division are inverse operations.
- Maintain equality by performing the same operation on both sides.
- Simplify both sides before isolating the variable by combining like terms.
Examples of Solving Linear Equations
- Solve for x: x + 5 = 12 => x = 12 - 5 => x = 7
- Solve for y: y - 3 = 8 => y = 8 + 3 => y = 11
- Solve for z: 4z = 20 => z = 20 / 4 => z = 5
- Solve for a: a / 2 = 9 => a = 9 * 2 => a = 18
- Solve for b: 2b + 3 = 11 => 2b = 11 - 3 => 2b = 8 => b = 8 / 2 => b = 4
Binomials
- A binomial is an algebraic expression containing two terms.
- Terms are connected by a plus or minus sign.
- Examples: x + y, a - b, 2m + 3n, p^2 - q^2.
Expanding Brackets
- Expanding brackets involves multiplying the outside term by each inside term.
- Use the distributive property: a(b + c) = ab + ac.
- Pay attention to signs when expanding.
Examples of Expanding Brackets
- Expand: 3(x + 2) = 3x + 6
- Expand: -2(y - 4) = -2y + 8
- Expand: a(2a + 5) = 2a^2 + 5a
- Expand: x(x - 3) = x^2 - 3x
- Expand: 5(2b + 1) = 10b + 5
Expanding Two Binomials
- Use FOIL (First, Outer, Inner, Last) or distributive property.
- (a + b)(c + d) = ac + ad + bc + bd
Examples of Expanding Two Binomials
- Expand: (x + 1)(x + 2) = x^2 + 2x + x + 2 = x^2 + 3x + 2
- Expand: (y - 3)(y + 4) = y^2 + 4y - 3y - 12 = y^2 + y - 12
- Expand: (2a + 1)(a - 2) = 2a^2 - 4a + a - 2 = 2a^2 - 3a - 2
- Expand: (b - 5)(b - 1) = b^2 - b - 5b + 5 = b^2 - 6b + 5
- Expand: (x + 3)(x - 3) = x^2 - 3x + 3x - 9 = x^2 - 9
Year 9 Level Algebra Questions
- Includes solving linear equations, simplifying expressions, expanding brackets, and basic factoring.
Simplifying Expressions
- Combine like terms.
- Like terms have the same variables to the same powers.
- Examples: 3x + 2x = 5x, 4y^2 - y^2 = 3y^2, 5ab + 2ab - ab = 6ab
Examples of Simplifying Expressions
- Simplify: 2x + 3y + 4x - y = 6x + 2y
- Simplify: 5a - 2b - 3a + 7b = 2a + 5b
- Simplify: 4m^2 + 2m - m^2 + 3m = 3m^2 + 5m
- Simplify: 7p - 3q + q - 4p = 3p - 2q
- Simplify: 6xy + 2x - 3xy + 4x = 3xy + 6x
Basic Factoring
- Breaking down an expression into its factors.
- Look for common factors.
- Examples: 4x + 8 = 4(x + 2), 3y^2 - 6y = 3y(y - 2)
Examples of Basic Factoring
- Factor: 5a + 10 = 5(a + 2)
- Factor: 2b - 6 = 2(b - 3)
- Factor: 4x^2 + 8x = 4x(x + 2)
- Factor: 6y - 9y^2 = 3y(2 - 3y)
- Factor: 7m^2 + 14m = 7m(m + 2)
Solving Equations with Fractions
- Eliminate fractions by multiplying by the least common denominator (LCD).
- LCD is the smallest multiple divisible by all denominators.
Examples of Solving Equations with Fractions
- Solve for x: x / 3 = 5 => x = 5 * 3 => x = 15
- Solve for y: 2y / 5 = 4 => 2y = 4 * 5 => 2y = 20 => y = 20 / 2 => y = 10
- Solve for z: (z + 1) / 2 = 3 => z + 1 = 3 * 2 => z + 1 = 6 => z = 6 - 1 => z = 5
- Solve for a: (a - 2) / 4 = 1 => a - 2 = 1 * 4 => a - 2 = 4 => a = 4 + 2 => a = 6
- Solve for b: (3b + 1) / 5 = 2 => 3b + 1 = 2 * 5 => 3b + 1 = 10 => 3b = 10 - 1 => 3b = 9 => b = 9 / 3 => b = 3
Quiz on Linear Equations, Binomials, Expanding Brackets, and Year 9 Algebra
- Consist of 30 questions focusing on linear equations, binomials, expanding brackets, and general year 9 level algebra.
- Questions should focus on direct algebraic manipulation and not be word problems.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.