Podcast
Questions and Answers
What is the symbol used to represent the union of sets A and B?
What is the symbol used to represent the union of sets A and B?
Which set operation creates a set containing elements that are common to sets A and B?
Which set operation creates a set containing elements that are common to sets A and B?
What does the symmetric difference of sets A and B contain?
What does the symmetric difference of sets A and B contain?
In Boolean algebra, what concept is closely connected to set theory?
In Boolean algebra, what concept is closely connected to set theory?
Signup and view all the answers
Which set operation forms a set containing elements unique to one set but not the other?
Which set operation forms a set containing elements unique to one set but not the other?
Signup and view all the answers
What do Venn diagrams visually represent?
What do Venn diagrams visually represent?
Signup and view all the answers
What does the intersection of two sets represent?
What does the intersection of two sets represent?
Signup and view all the answers
Which symbol represents the AND operation in Boolean algebra?
Which symbol represents the AND operation in Boolean algebra?
Signup and view all the answers
What does the complement of a set contain?
What does the complement of a set contain?
Signup and view all the answers
In a Venn diagram, what do overlapping regions represent?
In a Venn diagram, what do overlapping regions represent?
Signup and view all the answers
What does the OR operation in Boolean algebra correspond to in set theory?
What does the OR operation in Boolean algebra correspond to in set theory?
Signup and view all the answers
If the intersection of two sets is empty, what does it imply?
If the intersection of two sets is empty, what does it imply?
Signup and view all the answers
Study Notes
Set Theory: Exploring Operations, Diagrams, and Algebra
Set theory is a fundamental branch of mathematics that deals with the abstract concept of collections of objects, called sets. It provides a framework for understanding and organizing data structures and their relationships. In this article, we'll dive into the key aspects of set theory, focusing on set operations, Venn diagrams, the intersection of sets, the complement of sets, and their connections to Boolean algebra.
Set Operations
Set operations are the fundamental methods for manipulating and combining sets. There are four primary operations:
-
Union: This operation combines all elements from both sets, resulting in a set containing elements found in either or both original sets. The symbol for the union of sets A and B is A ∪ B.
-
Intersection: This operation creates a set containing elements that are common to both sets A and B. The symbol for the intersection of sets A and B is A ∩ B.
-
Difference: This operation forms a set containing elements that are unique to one set but not the other. The symbol for the difference of set A and set B is A - B.
-
Symmetric difference: This operation forms a set containing elements that are unique to either of the sets but not their intersection. The symbol for the symmetric difference of sets A and B is A Δ B.
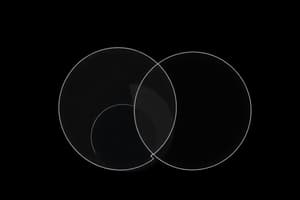
Venn Diagrams
Venn diagrams are visual representations of set operations, displaying the relationships between sets. Circles represent sets, and regions where circles overlap represent their intersection. Venn diagrams are a powerful tool for visualizing and understanding set theory concepts.
Intersection of Sets
The intersection of sets A and B, represented by A ∩ B, is the set of elements that are common to both sets. If the intersection is empty, the sets have no elements in common.
Complement of Sets
The complement of set A, denoted by A', contains all elements that are not in A. The universal set, denoted by U, represents all possible elements under consideration. The complement of A is defined relative to the universal set, A' = U - A.
Boolean Algebra
Set theory operations and Venn diagrams are closely related to Boolean algebra, a branch of mathematics that deals with logical operations. Boolean algebra can be represented using set theory, and set theory can be represented using Boolean algebra.
Boolean algebra has two primary operations:
-
AND: This operation is equivalent to the intersection operation in set theory. The symbol for the AND operation is ∧.
-
OR: This operation is equivalent to the union operation in set theory. The symbol for the OR operation is ∨.
Understanding the relationships between set theory, Venn diagrams, and Boolean algebra can help deepen your grasp of these fundamental mathematical concepts. As you delve deeper into set theory, you'll discover that its applications are widespread, including data analysis, computer science, and engineering. So, let's continue the journey to learn, explore, and apply these powerful mathematical tools to real-world problems.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Test your knowledge on set theory operations, Venn diagrams, intersections, complements, and their connections to Boolean algebra. Learn about fundamental methods for combining sets, visualizing relationships with Venn diagrams, and applying set theory concepts to logical operations in Boolean algebra.
