Podcast
Questions and Answers
Given that a body starts with an initial velocity of 0 m s-1 and accelerates uniformly to a velocity of 40 m s-1 in 10 seconds, what is the body's acceleration?
Given that a body starts with an initial velocity of 0 m s-1 and accelerates uniformly to a velocity of 40 m s-1 in 10 seconds, what is the body's acceleration?
The acceleration is 4 m s-2.
Using the same conditions as above, calculate the displacement of the body during this time.
Using the same conditions as above, calculate the displacement of the body during this time.
The displacement is 200 m.
What does the slope of a distance-time graph represent?
What does the slope of a distance-time graph represent?
The slope of a distance-time graph represents the velocity.
What is the significance of the area under a velocity-time graph?
What is the significance of the area under a velocity-time graph?
In a ticker tape experiment, how do you calculate the time taken for a set number of spaces on the tape?
In a ticker tape experiment, how do you calculate the time taken for a set number of spaces on the tape?
When calculating acceleration from initial and final velocities in a ticker tape experiment, which formula do you use?
When calculating acceleration from initial and final velocities in a ticker tape experiment, which formula do you use?
What precautions should be taken when using the meter stick to avoid errors in measurements?
What precautions should be taken when using the meter stick to avoid errors in measurements?
What condition must be met for the trolley on the sloped runway to maintain constant velocity?
What condition must be met for the trolley on the sloped runway to maintain constant velocity?
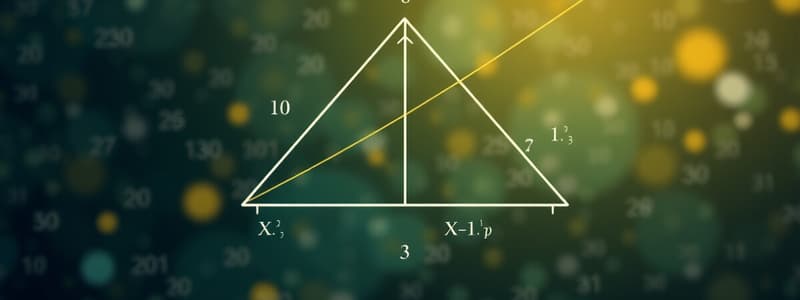
Using the Pythagorean theorem, how do you calculate the hypotenuse of a right triangle with sides of 7 m and 24 m?
Using the Pythagorean theorem, how do you calculate the hypotenuse of a right triangle with sides of 7 m and 24 m?
What distinguishes scalar quantities from vector quantities?
What distinguishes scalar quantities from vector quantities?
How do you derive the lengths of the other sides of a triangle when given an angle of 22.62° and a hypotenuse of 13 m?
How do you derive the lengths of the other sides of a triangle when given an angle of 22.62° and a hypotenuse of 13 m?
Explain the relationship between distance, time, and speed.
Explain the relationship between distance, time, and speed.
What are the vertical and horizontal components of a 25 N force applied at an angle of 16.26° to the horizontal?
What are the vertical and horizontal components of a 25 N force applied at an angle of 16.26° to the horizontal?
How is speed defined and how does it relate to velocity?
How is speed defined and how does it relate to velocity?
Using Pythagoras' Theorem, how can you find the length of the hypotenuse in a right-angled triangle?
Using Pythagoras' Theorem, how can you find the length of the hypotenuse in a right-angled triangle?
What is the formula to convert from kilometers per hour (km/h) to meters per second (m/s)?
What is the formula to convert from kilometers per hour (km/h) to meters per second (m/s)?
Describe the purpose of using trigonometric functions in relation to right-angled triangles.
Describe the purpose of using trigonometric functions in relation to right-angled triangles.
List three examples of scalar quantities and their SI units.
List three examples of scalar quantities and their SI units.
What is the relationship between acceleration, velocity, and time in linear motion?
What is the relationship between acceleration, velocity, and time in linear motion?
What role does SOHCAHTOA play in solving problems related to right-angled triangles?
What role does SOHCAHTOA play in solving problems related to right-angled triangles?
Which of the following is a scalar quantity?
Which of the following is a scalar quantity?
What is the SI unit for speed?
What is the SI unit for speed?
How does the distance relate to length as a scalar quantity?
How does the distance relate to length as a scalar quantity?
In the context of vector quantities, what is a resultant vector?
In the context of vector quantities, what is a resultant vector?
What does Pythagoras' Theorem state in relation to right-angled triangles?
What does Pythagoras' Theorem state in relation to right-angled triangles?
Which statement correctly defines a vector quantity?
Which statement correctly defines a vector quantity?
Which formula is represented by the mnemonic SOHCAHTOA for trigonometric functions?
Which formula is represented by the mnemonic SOHCAHTOA for trigonometric functions?
Which of the following is NOT an example of a scalar quantity?
Which of the following is NOT an example of a scalar quantity?
What unit is time measured in as a fundamental scalar quantity?
What unit is time measured in as a fundamental scalar quantity?
In a right-angled triangle with sides of lengths 7 m and 24 m, what is the length of the hypotenuse?
In a right-angled triangle with sides of lengths 7 m and 24 m, what is the length of the hypotenuse?
Which equation represents the relationship between the vertical component, its hypotenuse, and the angle in a vector resolution problem?
Which equation represents the relationship between the vertical component, its hypotenuse, and the angle in a vector resolution problem?
What is the average velocity when a body has an initial velocity of 10 m s-1 and a final velocity of 30 m s-1?
What is the average velocity when a body has an initial velocity of 10 m s-1 and a final velocity of 30 m s-1?
To convert a speed of 10 m s-1 to kilometers per hour, which calculation is correct?
To convert a speed of 10 m s-1 to kilometers per hour, which calculation is correct?
If a body has a constant acceleration of 2 m s-2, what is its velocity after 5 seconds if it starts from rest?
If a body has a constant acceleration of 2 m s-2, what is its velocity after 5 seconds if it starts from rest?
What is the result of resolving a vector into two components?
What is the result of resolving a vector into two components?
How is displacement defined in terms of direction and quantity?
How is displacement defined in terms of direction and quantity?
In the equations of motion, what does 's' represent?
In the equations of motion, what does 's' represent?
For a right-angled triangle, how do you find the lengths of the other two sides using a hypotenuse of 13 m and an angle of 22.62°?
For a right-angled triangle, how do you find the lengths of the other two sides using a hypotenuse of 13 m and an angle of 22.62°?
What is the primary purpose of using trigonometric functions in the context of right-angled triangles?
What is the primary purpose of using trigonometric functions in the context of right-angled triangles?
What is the correct formula to calculate the displacement if initial velocity, acceleration, and time are known?
What is the correct formula to calculate the displacement if initial velocity, acceleration, and time are known?
In a distance-time graph, the slope indicates which of the following?
In a distance-time graph, the slope indicates which of the following?
Which equation is used to relate final velocity squared to initial velocity squared, acceleration, and displacement?
Which equation is used to relate final velocity squared to initial velocity squared, acceleration, and displacement?
If a trolley moves down a sloped runway and accelerates, which of the following must be calculated for accurate results?
If a trolley moves down a sloped runway and accelerates, which of the following must be calculated for accurate results?
What is the primary purpose of measuring the distance between spaces on a ticker tape?
What is the primary purpose of measuring the distance between spaces on a ticker tape?
How can the area under a velocity-time graph be interpreted?
How can the area under a velocity-time graph be interpreted?
What unit is used to express acceleration in the context of motion?
What unit is used to express acceleration in the context of motion?
When calculating time using ticker tape, what does the formula t = n/f represent?
When calculating time using ticker tape, what does the formula t = n/f represent?
What does a constant slope on a distance-time graph indicate about motion?
What does a constant slope on a distance-time graph indicate about motion?
In the context of the experiments described, which of the following best describes the purpose of oiling the trolley wheels?
In the context of the experiments described, which of the following best describes the purpose of oiling the trolley wheels?
The acceleration of a body starting from rest and reaching a velocity of 40 m s-1 in 10 seconds is 6 m s-2.
The acceleration of a body starting from rest and reaching a velocity of 40 m s-1 in 10 seconds is 6 m s-2.
The displacement of a body that accelerates uniformly from rest to 40 m s-1 in 10 seconds is 200 m.
The displacement of a body that accelerates uniformly from rest to 40 m s-1 in 10 seconds is 200 m.
The slope of a velocity-time graph represents the distance travelled by an object.
The slope of a velocity-time graph represents the distance travelled by an object.
When using ticker tape, the time taken for a set number of spaces is calculated by dividing the number of spaces by the oscillating frequency of the timer.
When using ticker tape, the time taken for a set number of spaces is calculated by dividing the number of spaces by the oscillating frequency of the timer.
To maintain a constant velocity on a sloped runway, the frictional force must be greater than the gravitational force acting on the trolley.
To maintain a constant velocity on a sloped runway, the frictional force must be greater than the gravitational force acting on the trolley.
The letter 's' in the equations of motion typically represents speed.
The letter 's' in the equations of motion typically represents speed.
If the distance between spaces on a ticker tape is constant, the object is moving at a constant velocity.
If the distance between spaces on a ticker tape is constant, the object is moving at a constant velocity.
The formula for acceleration is given by $a = \frac{v}{t}$.
The formula for acceleration is given by $a = \frac{v}{t}$.
When measuring the displacement using the formula $s = ut + \frac{1}{2}at^2$, if the initial velocity 'u' is zero, the equation simplifies to $s = \frac{1}{2}at^2$.
When measuring the displacement using the formula $s = ut + \frac{1}{2}at^2$, if the initial velocity 'u' is zero, the equation simplifies to $s = \frac{1}{2}at^2$.
Flashcards are hidden until you start studying
Study Notes
Scalar and Vector Quantities
- Scalar quantities have magnitude only and no direction. Examples include length, mass, time, area, density, energy, electric charge, volume, pressure, work, speed, temperature, and power.
- Vector quantities possess both magnitude and direction. Examples include displacement, velocity, acceleration, momentum, force, and electric field strength.
Distances, Time, and Speed
- Distance (s) measures how far apart two points are, often termed length (l), with SI unit meters (m).
- Time (t) is a scalar measuring duration, with SI unit seconds (s), typically measured using stopwatches or timers.
- Speed (v), a scalar quantity, is calculated as distance per unit time, measured in meters per second (m/s).
Pythagoras’ Theorem and Trigonometric Functions
- Pythagoras’ Theorem states: Hypotenuse² = Opposite² + Adjacent².
- Trigonometric ratios for a right-angled triangle:
- Sine: sin(θ) = Opposite/Hypotenuse
- Cosine: cos(θ) = Adjacent/Hypotenuse
- Tangent: tan(θ) = Opposite/Adjacent
- SOHCAHTOA is a mnemonic for remembering these relationships.
Vector Resolution
- Vectors can be resolved into two components using trigonometry based on their angle with respect to the horizontal.
- For a vector of magnitude F at an angle θ:
- Vertical component = F sin(θ)
- Horizontal component = F cos(θ)
Motion and Acceleration
- Acceleration (a) is the rate of change of velocity, with SI unit meters per second squared (m/s²).
- Basic equations of motion for linear acceleration are derived from definitions of velocity and displacement:
- v = u + at
- v² = u² + 2as
- s = ut + ½at²
Conversions Between Speed Units
- Conversion from km/h to m/s: Divide by 3.6.
- Conversion from m/s to km/h: Multiply by 3.6.
Distance-Time and Velocity-Time Graphs
- The slope of a distance-time graph indicates velocity.
- The slope of a velocity-time graph indicates acceleration, while the area under it equals distance traveled.
Practical Measurements
- Using ticker tape and a timer can help measure and calculate velocity and acceleration by observing the distance between tape dots over time.
- Ensuring proper conditions during experiments is crucial for accurate results, such as reducing friction and avoiding parallax errors.
Sample Problems
- Real-world applications of these concepts demonstrate the importance of understanding motion, such as calculating displacement and acceleration based on given initial conditions and forces.
Summary
- Mastery of scalar and vector quantities, their relationships, measurement techniques, and equations of motion enables a comprehensive understanding of kinematics essential for physics studies.
Scalar and Vector Quantities
- Scalar quantities have magnitude only and no direction. Examples include length, mass, time, area, density, energy, electric charge, volume, pressure, work, speed, temperature, and power.
- Vector quantities possess both magnitude and direction. Examples include displacement, velocity, acceleration, momentum, force, and electric field strength.
Distances, Time, and Speed
- Distance (s) measures how far apart two points are, often termed length (l), with SI unit meters (m).
- Time (t) is a scalar measuring duration, with SI unit seconds (s), typically measured using stopwatches or timers.
- Speed (v), a scalar quantity, is calculated as distance per unit time, measured in meters per second (m/s).
Pythagoras’ Theorem and Trigonometric Functions
- Pythagoras’ Theorem states: Hypotenuse² = Opposite² + Adjacent².
- Trigonometric ratios for a right-angled triangle:
- Sine: sin(θ) = Opposite/Hypotenuse
- Cosine: cos(θ) = Adjacent/Hypotenuse
- Tangent: tan(θ) = Opposite/Adjacent
- SOHCAHTOA is a mnemonic for remembering these relationships.
Vector Resolution
- Vectors can be resolved into two components using trigonometry based on their angle with respect to the horizontal.
- For a vector of magnitude F at an angle θ:
- Vertical component = F sin(θ)
- Horizontal component = F cos(θ)
Motion and Acceleration
- Acceleration (a) is the rate of change of velocity, with SI unit meters per second squared (m/s²).
- Basic equations of motion for linear acceleration are derived from definitions of velocity and displacement:
- v = u + at
- v² = u² + 2as
- s = ut + ½at²
Conversions Between Speed Units
- Conversion from km/h to m/s: Divide by 3.6.
- Conversion from m/s to km/h: Multiply by 3.6.
Distance-Time and Velocity-Time Graphs
- The slope of a distance-time graph indicates velocity.
- The slope of a velocity-time graph indicates acceleration, while the area under it equals distance traveled.
Practical Measurements
- Using ticker tape and a timer can help measure and calculate velocity and acceleration by observing the distance between tape dots over time.
- Ensuring proper conditions during experiments is crucial for accurate results, such as reducing friction and avoiding parallax errors.
Sample Problems
- Real-world applications of these concepts demonstrate the importance of understanding motion, such as calculating displacement and acceleration based on given initial conditions and forces.
Summary
- Mastery of scalar and vector quantities, their relationships, measurement techniques, and equations of motion enables a comprehensive understanding of kinematics essential for physics studies.
Scalar and Vector Quantities
- Scalar quantities have magnitude only and no direction. Examples include length, mass, time, area, density, energy, electric charge, volume, pressure, work, speed, temperature, and power.
- Vector quantities possess both magnitude and direction. Examples include displacement, velocity, acceleration, momentum, force, and electric field strength.
Distances, Time, and Speed
- Distance (s) measures how far apart two points are, often termed length (l), with SI unit meters (m).
- Time (t) is a scalar measuring duration, with SI unit seconds (s), typically measured using stopwatches or timers.
- Speed (v), a scalar quantity, is calculated as distance per unit time, measured in meters per second (m/s).
Pythagoras’ Theorem and Trigonometric Functions
- Pythagoras’ Theorem states: Hypotenuse² = Opposite² + Adjacent².
- Trigonometric ratios for a right-angled triangle:
- Sine: sin(θ) = Opposite/Hypotenuse
- Cosine: cos(θ) = Adjacent/Hypotenuse
- Tangent: tan(θ) = Opposite/Adjacent
- SOHCAHTOA is a mnemonic for remembering these relationships.
Vector Resolution
- Vectors can be resolved into two components using trigonometry based on their angle with respect to the horizontal.
- For a vector of magnitude F at an angle θ:
- Vertical component = F sin(θ)
- Horizontal component = F cos(θ)
Motion and Acceleration
- Acceleration (a) is the rate of change of velocity, with SI unit meters per second squared (m/s²).
- Basic equations of motion for linear acceleration are derived from definitions of velocity and displacement:
- v = u + at
- v² = u² + 2as
- s = ut + ½at²
Conversions Between Speed Units
- Conversion from km/h to m/s: Divide by 3.6.
- Conversion from m/s to km/h: Multiply by 3.6.
Distance-Time and Velocity-Time Graphs
- The slope of a distance-time graph indicates velocity.
- The slope of a velocity-time graph indicates acceleration, while the area under it equals distance traveled.
Practical Measurements
- Using ticker tape and a timer can help measure and calculate velocity and acceleration by observing the distance between tape dots over time.
- Ensuring proper conditions during experiments is crucial for accurate results, such as reducing friction and avoiding parallax errors.
Sample Problems
- Real-world applications of these concepts demonstrate the importance of understanding motion, such as calculating displacement and acceleration based on given initial conditions and forces.
Summary
- Mastery of scalar and vector quantities, their relationships, measurement techniques, and equations of motion enables a comprehensive understanding of kinematics essential for physics studies.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.