Podcast
Questions and Answers
If for a square matrix A, A. (adjA) = [2025 0 0
0 2025 0
0 0 2025], then the value of |A| + |adj A| is equal to:
If for a square matrix A, A. (adjA) = [2025 0 0 0 2025 0 0 0 2025], then the value of |A| + |adj A| is equal to:
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k, respectively. Then the restriction on n, k and p so that PY + WY will be defined are:
Assume X, Y, Z, W and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3 and p × k, respectively. Then the restriction on n, k and p so that PY + WY will be defined are:
The interval in which the function f defined by f(x) = e^x is strictly increasing, is
The interval in which the function f defined by f(x) = e^x is strictly increasing, is
If A and B are non-singular matrices of same order with det(A) = 5, then det(B⁻¹AB) is equal to
If A and B are non-singular matrices of same order with det(A) = 5, then det(B⁻¹AB) is equal to
Signup and view all the answers
The value of 'n', such that the differential equation xⁿ dy/dx = y(logy - logx + 1); (where x, y ∈ R⁺) is homogeneous, is
The value of 'n', such that the differential equation xⁿ dy/dx = y(logy - logx + 1); (where x, y ∈ R⁺) is homogeneous, is
Signup and view all the answers
If the points (x₁, y₁), (x₂, y₂) and (x₁ + x₂, y₁ + y₂) are collinear, then x₁y₂ is equal to
If the points (x₁, y₁), (x₂, y₂) and (x₁ + x₂, y₁ + y₂) are collinear, then x₁y₂ is equal to
Signup and view all the answers
If A = [-1 a 0
2 3 -b] is a skew-symmetric matrix then the value of a + b + c =
If A = [-1 a 0 2 3 -b] is a skew-symmetric matrix then the value of a + b + c =
Signup and view all the answers
For any two events A and B, if P(A) = 1/3, P(B) = 2/3 and P(A ∩ B) = 1/4, then P(A/B) equals:
For any two events A and B, if P(A) = 1/3, P(B) = 2/3 and P(A ∩ B) = 1/4, then P(A/B) equals:
Signup and view all the answers
The value of a if the angle between p = 2a²î - 3aĵ + k and q = î + ĵ + ak is obtuse, is
The value of a if the angle between p = 2a²î - 3aĵ + k and q = î + ĵ + ak is obtuse, is
Signup and view all the answers
If |a| = 3, |b| = 4 and |a + b| = 5, then |a - b| =
If |a| = 3, |b| = 4 and |a + b| = 5, then |a - b| =
Signup and view all the answers
For the linear programming problem (LPP), the objective function is Z = 4x + 3y and the feasible region determined by a set of constraints is shown in the graph.
[Diagram of a graph with points P(0,40), Q(30,20), R(40,0) and O(0,0) marked].
Which of the following statements is true?
For the linear programming problem (LPP), the objective function is Z = 4x + 3y and the feasible region determined by a set of constraints is shown in the graph.
[Diagram of a graph with points P(0,40), Q(30,20), R(40,0) and O(0,0) marked].
Which of the following statements is true?
Signup and view all the answers
∫ dx / x³(1+x⁴)² equals
∫ dx / x³(1+x⁴)² equals
Signup and view all the answers
∫₂⁰ cosec²x dx =
∫₂⁰ cosec²x dx =
Signup and view all the answers
What is the general solution of the differential equation e^y' = x?
What is the general solution of the differential equation e^y' = x?
Signup and view all the answers
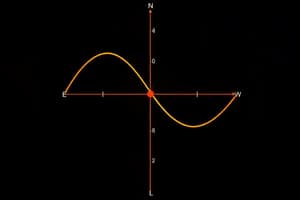
The graph drawn below depicts [Graph shows a curve that looks like y = cos⁻¹x]
The graph drawn below depicts [Graph shows a curve that looks like y = cos⁻¹x]
Signup and view all the answers
A linear programming problem (LPP) along with the graph of its constraints is shown below. [Diagram of a graph with points A(15,0), B1(0,10), B2(0,20), P(3,8) and O(0,0) marked, showing a shaded feasible region]. The corresponding objective function is Z = 18x + 10y, which has to be minimized. The smallest value of the objective function Z is 134 and is obtained at the corner point (3, 8).
The optimal solution of the above linear programming problem
A linear programming problem (LPP) along with the graph of its constraints is shown below. [Diagram of a graph with points A(15,0), B1(0,10), B2(0,20), P(3,8) and O(0,0) marked, showing a shaded feasible region]. The corresponding objective function is Z = 18x + 10y, which has to be minimized. The smallest value of the objective function Z is 134 and is obtained at the corner point (3, 8).
The optimal solution of the above linear programming problem
Signup and view all the answers
The function f: R → Z defined by f(x) = [x], where [.] denotes the greatest integer function, is
The function f: R → Z defined by f(x) = [x], where [.] denotes the greatest integer function, is
Signup and view all the answers
A student observes an open-air Honeybee nest on the branch of a tree, whose plane figure is parabolic shape given by x² = 4y. Then the area (in sq units) of the region bounded by parabola x² = 4y and the line y = 4 is
A student observes an open-air Honeybee nest on the branch of a tree, whose plane figure is parabolic shape given by x² = 4y. Then the area (in sq units) of the region bounded by parabola x² = 4y and the line y = 4 is
Signup and view all the answers
Consider the function defined as f(x) = |x| + |x - 1|, x ∈ R. Then f(x) is not differentiable at x = 0 and x = 1.
Consider the function defined as f(x) = |x| + |x - 1|, x ∈ R. Then f(x) is not differentiable at x = 0 and x = 1.
Signup and view all the answers
The function f: R → (-∞, -1] U [1, ∞) defined by f(x) = secx is not one-one function in its domain.
The function f: R → (-∞, -1] U [1, ∞) defined by f(x) = secx is not one-one function in its domain.
Signup and view all the answers
If cot⁻¹(3x + 5) > π/6, then find the range of the values of x.
If cot⁻¹(3x + 5) > π/6, then find the range of the values of x.
Signup and view all the answers
The cost (in rupees) of producing x items in factory, each day is given by C(x) = 0.00013x³ + 0.002x² + 5x + 2200. Find the marginal cost when 150 items are produced.
The cost (in rupees) of producing x items in factory, each day is given by C(x) = 0.00013x³ + 0.002x² + 5x + 2200. Find the marginal cost when 150 items are produced.
Signup and view all the answers
(a) Find the derivative of tan⁻¹x with respect to logx, where x ∈ (1, ∞).
(a) Find the derivative of tan⁻¹x with respect to logx, where x ∈ (1, ∞).
Signup and view all the answers
Study Notes
Section A - Multiple Choice Questions
- Question 1: If a square matrix A satisfies A(adj A) = 0, then |A| + |adj A| equals 2025.
- Question 2: For matrices X, Y, Z, W, and P of given orders, the restriction for PY + WY to be defined is k = 3 and p = n.
- Question 3: The function f(x) = ex is strictly increasing for all x ∈ ( -∞, ∞).
Section B - Very Short Answer Questions
- Question 21: To satisfy cot-1(3x + 5) > 0, the range of x values needs to be found.
- Question 22: Marginal cost at 150 items produced is calculated from the cost function given.
- Question 23: a) The derivative of tan-1x w.r.t. logx is 1/(1 + x2) / (1/x) = x/(1 + x2). b) The derivative of (cosx)x with respect to x is given.
- Question 24: a) If b + 2c is perpendicular to a, then the value of λ needs to be solved for. b) The angles that BA makes with the x,y, and z axes need to be determined.
- Question 25: The diagonals and area of a parallelogram with given sides are to be calculated.
Section C - Short Answer Questions
- Question 26: The rate at which a kite's string is released is found using related rates.
- Question 27: The rate of increase in spatial ability understanding decreases as age increases.
- Question 28: a)The angle θ and scalar projection of T on T2 are determined. b) The vector and Cartesian equations of a line passing through a given point and perpendicular to two given lines are to be determined
- Question 29: a) The integral ∫1∞ (log x)/(log x)2 dx is evaluated. b)∫01 xn(1 - x)m dx is evaluated.
- Question 30: The minimum value of Z = x + 2y, subject to constraints, is graphically shown to occur at more than two points.
- Question 31: a) The probability that it will not rain today is P1. The probability that it will rain tomorrow given that it did not rain today is P3. b) The probability that condition is met is to be determined. Or, a random variable (X) takes non-negative integral values and probability (pn) is proportional to 5-n .
Section D - Long Answer Questions
- Question 32: The area under the curve y = 20cos2x from x=π/6 to x=π/3 is determined.
- Question 33: The values of a, b, and c in the equation of the path of a ball are determined using matrices. The equation is found.
- Question 34: a) The second derivative of f(x) = |x|3 is found showing that it exists for all real x. b) If (x - a)² + (y - b)² = c² then the second derivative of y with respect to x is determined for some constant c > 0.
- Question 35: a) The shortest distance between two given lines is to be found. b) The image of a point with respect to a line and the equation of the joining line are determined.
Section E - Case Study Questions
- Question 36: a) Volume of a container as a function of x is to be determined b) The derivative of the volume is found. c) The maximum value of x, and whether V has a point of inflection, are to be found.
- Question 37: a) Number of possible relations from set B to set G is found. b) The smallest equivalence relation on set G is to be written. c) The relation on set B is altered to meet specific criteria (reflexive, symmetric,transitive) d) Whether the track function is one-to-one and onto is to be checked.
- Question 38: a) The probability that the owl is still in Cage I, given two birds fly from one cage to the other is determined. b) The probability that one parrot and the owl flew from Cage-I to Cage-II, given a condition involving simultaneous flying of two birds are determined.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Related Documents
Description
Test your understanding of key concepts in mathematics for Class 12. This quiz covers multiple choice and very short answer questions relating to matrices, derivatives, and functions. Challenge yourself with varying difficulty to reinforce your knowledge and problem-solving skills.
