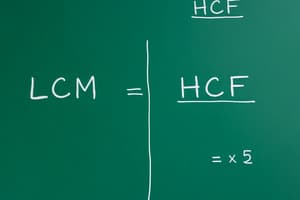Podcast
Questions and Answers
What are the steps involved in calculating the LCM using the listing multiples method?
What are the steps involved in calculating the LCM using the listing multiples method?
List the multiples of each number and identify the smallest multiple that appears in all lists.
How do you find the LCM using prime factorization?
How do you find the LCM using prime factorization?
Factor each number into prime factors, take the highest powers of each distinct prime factor, and multiply them together.
Describe the relationship between LCM and GCD when calculating LCM using the GCD method.
Describe the relationship between LCM and GCD when calculating LCM using the GCD method.
The LCM can be found using the formula LCM(a, b) = (a × b) / GCD(a, b).
In the ladder method, what do you do after dividing the given numbers by common prime factors?
In the ladder method, what do you do after dividing the given numbers by common prime factors?
Signup and view all the answers
Why might the GCD method be more efficient for larger numbers when calculating LCM?
Why might the GCD method be more efficient for larger numbers when calculating LCM?
Signup and view all the answers
What should you do to ensure accuracy when using the prime factorization method for LCM?
What should you do to ensure accuracy when using the prime factorization method for LCM?
Signup and view all the answers
Study Notes
Lowest Common Multiple (LCM)
Definition
- The Lowest Common Multiple (LCM) of two or more integers is the smallest multiple that is evenly divisible by each of the integers.
Methods for Calculating LCM
-
Listing Multiples
- List the multiples of each number.
- Identify the smallest multiple that appears in all lists.
- Example: For 4 and 5.
- Multiples of 4: 4, 8, 12, 16, 20...
- Multiples of 5: 5, 10, 15, 20...
- LCM is 20.
-
Prime Factorization
- Factor each number into its prime factors.
- For each distinct prime factor, take the highest power that appears in any of the factorizations.
- Multiply these together to get the LCM.
- Example: For 12 and 18.
- 12 = 2² × 3¹
- 18 = 2¹ × 3²
- LCM = 2² × 3² = 36.
-
Using the Greatest Common Divisor (GCD)
- Use the relationship: LCM(a, b) = (a × b) / GCD(a, b).
- Calculate the GCD first, then apply the formula.
- Example: For 8 and 12.
- GCD(8, 12) = 4
- LCM(8, 12) = (8 × 12) / 4 = 24.
-
Using the Ladder Method (Division Method)
- Write the numbers in a row.
- Divide by common prime factors until only 1s remain.
- Multiply all the divisors used.
- Example: For 6 and 8.
- 2 | 6 8
- 3 | 3 4
- 4 | 1 1
- LCM = 2 × 2 × 3 = 12.
Tips for Efficient Calculation
- Start with the method that best suits the numbers involved (e.g., for large numbers, GCD method may be more efficient).
- Ensure all factors are accounted for when using prime factorization.
- Practice with various sets of numbers to become comfortable with each method.
Lowest Common Multiple (LCM)
- The Lowest Common Multiple (LCM) is the smallest multiple shared by two or more integers, ensuring each integer can divide it without a remainder.
Methods for Calculating LCM
-
Listing Multiples
- Identify multiples for each number and find the smallest shared multiple.
- For example, multiples of 4 are 4, 8, 12, 16, 20, while multiples of 5 are 5, 10, 15, 20. The LCM is 20.
-
Prime Factorization
- Decompose each number into prime factors.
- For distinct prime factors, take the highest power from any factorization.
- Example:
- For 12: (12 = 2^2 × 3^1)
- For 18: (18 = 2^1 × 3^2)
- LCM is (2^2 × 3^2 = 36).
-
Using the Greatest Common Divisor (GCD)
- Apply the relationship: LCM(a, b) = (a × b) / GCD(a, b).
- Calculate the GCD first; then use the formula.
- Example: For 8 and 12, GCD(8, 12) = 4, LCM(8, 12) = (8 × 12) / 4 = 24.
-
Using the Ladder Method (Division Method)
- Arrange numbers in a row and divide by common prime factors until reduced to 1s.
- Multiply the divisors used to find the LCM.
- Example: For 6 and 8:
- Step 1: 2 | 6 8
- Step 2: 3 | 3 4
- Step 3: 4 | 1 1
- LCM = (2 × 2 × 3 = 12).
Tips for Efficient Calculation
- Choose a method based on the size of numbers involved; the GCD method may be preferable for larger numbers.
- Ensure all prime factors are accounted for when using prime factorization.
- Regular practice with different number sets enhances proficiency with each method.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Description
Test your understanding of the Lowest Common Multiple (LCM) through various calculation methods. This quiz covers methods such as listing multiples, prime factorization, and using the Greatest Common Divisor (GCD). Sharpen your skills with practical examples and calculations.
